线段树浅记

夏佑 | XiaU
  2023-07-23 2023-07-23 创建   2024-11-07 09:43:12 2024-11-07 09:43:12 更新      19.8k 字  90 分钟  

线段树浅记 ~ 从 0 开始的线段树生活

系统复盘了一下线段树，发现网上现有博客鲜有将线段树各种操作一步一步讲明白的，故结合自己理解写此文。

线段树

先来看一个经典问题：

给定序列 \(\{a_n\}\)，\(q\) 次操作，每次操作诸如：

1 x v：给 \(a_x\) 加上 \(v\)；

2 l r：查询区间 \([l,r]\) 的和。

\(1\leq n,q\leq 10^5\)。

考虑最朴素的暴力：对于 \(1\) 操作，直接在数组上更改。对于每次 \(2\) 操作，我们暴力遍历一遍整个数组。这样单次修改复杂度是 \(O(1)\)，但是查询复杂度是 \(O(n)\)，最坏时间复杂度 \(O(nq)\)，比较爆炸。

线段树作为一种基础的高级数据结构，具有单次修改、查询均为 \(O(\log n)\) 的优秀复杂度。这时候运用线段树，就比较好解决这个问题了。

结构

我们先来说一下线段树的结构。

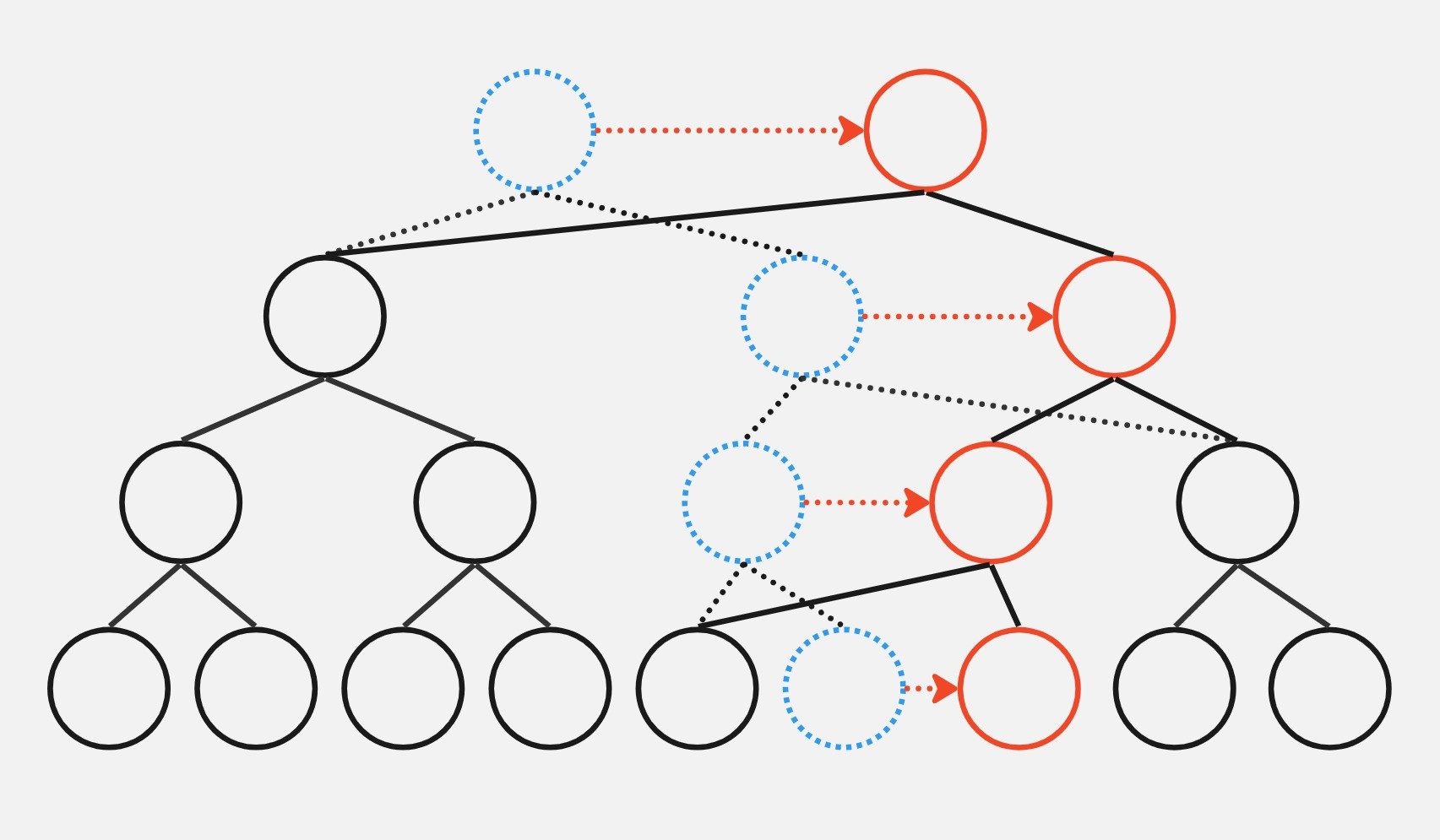
线段树

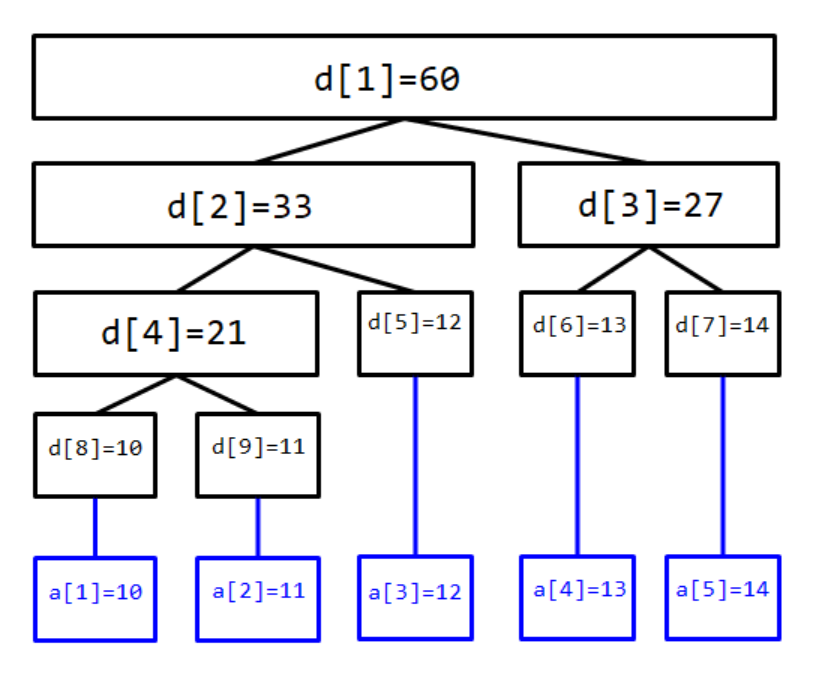
考虑现在有一段长度为 \(5\) 的区间 \([1,5]\)，我们递归地每次分成两半。

第一层：\([1,5]\)，第二层：\([1,3],[4,5]\)，以此类推……

现在 \(d_1\) 就记录着区间 \([1,5]\) 的信息，\(d_2\) 记录着 \([1,3]\) 的信息，以此类推。这个信息可以是多种多样的，根据本题的题意，我们可以记录“区间和”这个信息。此时，\(d_1\) 就表示着区间 \([1,5]\) 的和为 \(60\)。

显然，我们现在的 \(d\) 数组构成了一个二叉树型结构，\(d_1\) 的儿子是 \(d_2\) 和 \(d_3\)，\(d_2\) 的儿子是 \(d_4\) 和 \(d_5\)。那么根据二叉树的性质，我们很容易可以知道，若父亲节点的编号是 \(k\)，那么它的左儿子的节点编号应该是 \(2k\)，右儿子的节点编号应该是 \(2k+1\)。

这样，一颗线段树的基本结构就出来了。

考虑一下我们需要维护哪些信息？首先，区间和 \(sum\)。其次，我们需要维护当前节点所维护区间的左右端点 \(l,r\)。

1
2
3
4
5
struct Tree
{
    int l, r;
    int sum;
}tr[MAXN << 2];

哎？你这个 \(tr\) 数组怎么开了 \(4\) 倍的空间啊？线段树节点数量不是 \(2n\) 的吗？

我们理想的线段树形态应该是一棵满二叉树。此时，节点数量就是完美的 \(2n\) 个了。但是有时事与愿违。我们采用的编号方法是左儿子 \(2k\)，右儿子 \(2k+1\)，这样当我们原区间不是 \(2^m\) 的时候就会发生“左偏”（如上图）。

容易发现：左儿子和右儿子层数最多相差一。因此，我们线段树的节点有可能会延伸到叶子节点下面的一层，所以需要多开 \(2n\) 个节点，即 \(4n\)。

或者，我们有一个更加数学化的说明：线段树的节点应当是 \(1+2+4+\cdots +2^{\lceil\log _2 n\rceil}<4n\) 个。

注：无特殊说明外，本文 \(\log\) 均为 \(\log_2\)。

信息的上传

然而，我们现在的线段树只是一颗线段树，跟原来的序列没有啥关系啊？

考虑这颗线段树的叶子节点。我们发现叶子节点维护的区间都只有一个数，那么这个就对应着我们原序列的值。也就是说，左右端点均为 \(i\) 的线段树节点，其区间和就是 \(a_i\) 的值。

然后我们需要让整棵树都维护正确的信息，这时候就需要我们把信息由下到上地更新。我们记载的信息是区间和，那么显然，父亲节点的信息就是儿子节点信息之和，也就是说：\(tr[k].sum=tr[ls(k)].sum+tr[rs(k)].sum\)。

注：下文将用 \(tr\) 代替 \(d\)。

这里的 \(ls(k) = 2k, rs(k) = 2k+1\)，分别表示了当前节点的左右儿子。

1
2
3
4
5
6
7
8
9
#define ls (k << 1)
#define rs (k << 1 | 1)
//常用技巧，使用#define会让你的代码更美丽
//根据基本的位运算常识，k<<1=2k, k<<1|1=2k+1

void pushup(int k)
{
    tr[k].sum = tr[ls].sum + tr[rs].sum;
}

建树

著名感情学家鸭子曾经说过：我们要有所建树。不建树是一个线段树题目中常见的**错误。

考虑我们是怎么讲述一颗线段树的结构的？\(d_1\) 记录着整个区间的信息，然后每次将区间分成两半，分别记录着左右两半区间的信息……

那么参照这个思想，我们就可以建树了。从 \(d_1\) 出发，依次建立左右儿子的初始信息，然后 \(pushup\)，把下层的节点信息上传到上层。对于叶子节点，此时显然一定有 \(tr[k].l=tr[k].r\)，\(tr[k].sum=a[l]\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void build(int k, int l, int r)
{
    tr[k].l = l;
    tr[k].r = r;
    if(l == r)
    {
        tr[k].sum = a[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(ls, l, mid);
    build(rs, mid + 1, r);
    pushup(k);
}

时间复杂度显然 \(O(n)\)。

单点修改

好了，现在树也建好了，是时候干点操作相关的事情了。单点修改！

这个东西有点像二分。由于我们只修改一个点，那么我们只需要每次看看这个点在左右两半区间的那边，然后一直到叶子的时候把它修改了，再更新一下整棵树就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
void update(int k, int x, int v)
{
    if(tr[k].l == tr[k].r)
    {
        tr[k].sum += v;
        return;
    }
    int mid = (tr[k].l + tr[k].r) >> 1;
    if(x <= mid) update(ls, x, v);
    else update(rs, x, v);
    pushup(k);
}

由于我们最多跳 \(\log(n)\) 次，因此单点修改的时间复杂度是 \(O(\log n)\) 的。

区间查询

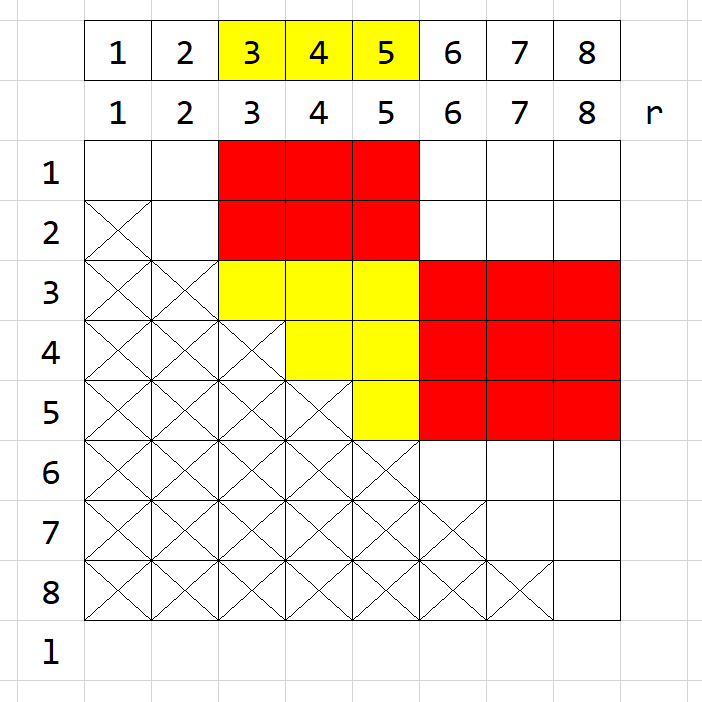
那么接下来解决最后一个问题：区间查询。

线段树

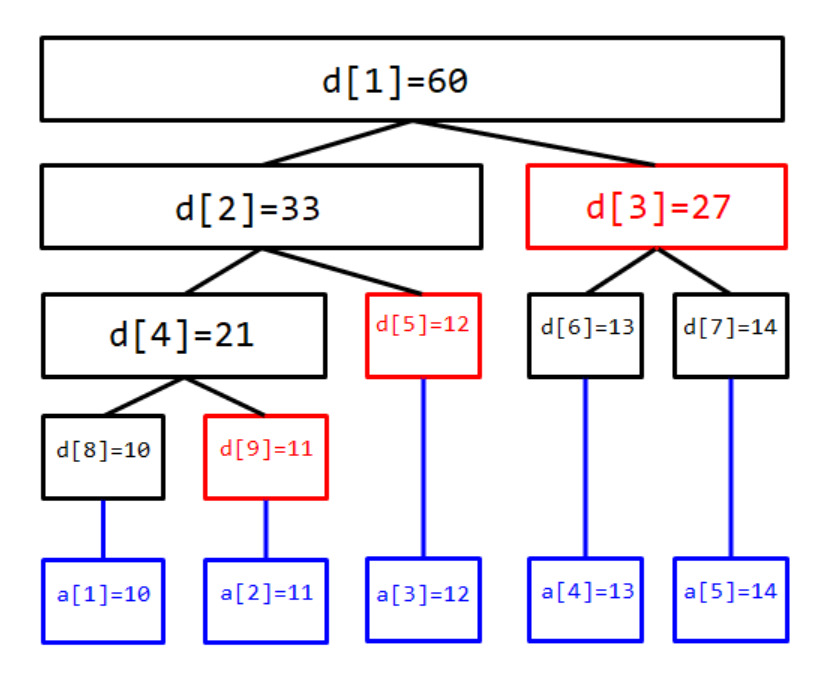
再看一眼这张图。如果我们要查询区间 \([2,5]\) 的值，那么比较理想的状态应该是什么？

应该是，我们每次找到可以被询问区间包含的极大区间，最后将所有区间的信息相加。

太抽象了？让我们具体看看。

从第一层开始：\([1,5]\) 的信息显然太大了，我们用不了，那么往下面找。

现在我们有区间 \([1,3]\) 和 \([4,5]\) 的信息。我们发现 \([2,5]\) 完全包含 \([4,5]\)，也就是说 \([4,5]\) 的信息可以被我们利用，那么就算上它的区间和。那啥叫极大呢？我们发现利用 \([4,5]\) 的信息显然比分别利用 \([4,4]\) 和 \([5,5]\) 要更优。意思就是：我们能用父亲的信息，就不用儿子的信息。

继续，我们现在还差 \([2,3]\) 的信息没解决。由于右边已经完成了，那么我们直接在左边找就可以。第三层是 \([1,2]\) 和 \([3,3]\)，其中我们可以用 \([3,3]\) 的信息，把它加上。

然后我们继续往下找，发现了 \([1,1]\) 和 \([2,2]\)，其中我们可以利用 \([2,2]\) 的信息，那就把它加上。

最后，我们发现区间 \([2,5]\) 实际上被拆成了 \([2,2] \cup [3,3]\cup [4,5]\)，我们所求的答案自然就是这几个节点的信息之和。

那么考虑一下我们应该怎么写代码：如果当前节点的区间被询问区间完全包含，那么直接加上这个区间的信息。否则，如果查询区间的左端点在左儿子内，就到左儿子内中继续查询；如果查询区间的右端点在右儿子内，就到右儿子内中继续查询。

1
2
3
4
5
6
7
8
9
int query(int k, int l, int r)
{
    int res = 0;
    if(l <= tr[k].l && tr[k].r <= r) return tr[k].sum;
    int mid = (tr[k].l + tr[k].r) >> 1;
    if(l <= mid) res += query(ls, l, r);
    if(r > mid) res += query(rs, l, r);
    return res;
}

来分析一下时间复杂度：由于线段树只有 \(\log(n)\) 层，那么我们也只需要询问 \(O(\log n)\) 次，单次区间查询时间复杂度是 \(O(\log n)\)。

区间修改与懒标记

那么现在我们把这个问题进阶一下：

给定序列 \(\{a_n\}\)，\(q\) 次操作，每次操作诸如：

1 l r v：给区间 \([l,r]\) 的每个元素加上 \(v\)；

2 l r：查询区间 \([l,r]\) 的和。

\(1\leq n,q\leq 10^5\)。

现在，我们由单点修改变成了区间修改。

问题在哪？我们每次修改，如果一个区间被修改区间包含，那么以它为根的整棵子树都要被修改，时间复杂度到了 \(O(n)\)，这是我们无法接受的。

哎？同样是涉及到区间，那为啥区间查询的复杂度很对，但是区间修改就很寄呢？

我们发现，区间查询的时候，如果一个节点被用到了，那么它的儿子就不会在被查询，因此时间复杂度可以到 \(O(\log n)\)。那我们能不能类比区间查询，让区间修改也这样呢？

这个时候就需要懒标记(lazy tag)出场了。

懒标记，顾名思义，是为了偷懒用的标记。

怎么偷懒呢？当我们遇到一个被修改区间完全包含的区间的时候，我们就给这个节点打上一个标记，意思是：我这个节点的后代应该被这个标记影响，但是我现在先不往下传。（我知道你很急，但是你先别急） 到我什么时候要用到这个节点的后代的时候，我再把标记传下去。

这样的话，我们就可以保证区间修改的时间复杂度为 \(O(\log n)\)。

那么具体怎么实现呢？

当我们区间修改遇到一个整的区间时，我们选择仅更改当前的节点的值，并给它打上懒标记。以区间和为例，我们更改当前节点的值显然应当是 \(v*(tr[k].r-tr[k].l+1)\)，此时我们把当前节点的 \(tag\) 加上 \(v\)，表示我后面的后代应当被加 \(v\)。

然后我们想想怎么把标记下放。显然我们只需要把标记分别赋给他的两个儿子，然后把当前节点的标记清零就可以了。考虑一下，那些操作需要把标记下放？

由于需要用到后代的操作都需要下方，所以显然查询和修改都需要提前下放标记。显然，标记的下放必须在操作之前。

那么我们就可以开始写代码了。首先先单独写一个下放标记的函数pushdown：

1
2
3
4
5
6
7
8
void pushdown(int k)
{
    tr[ls].tag += tr[k].tag;
    tr[rs].tag += tr[k].tag;
    tr[ls].sum += (tr[ls].r - tr[ls].l + 1) * tr[k].tag;
    tr[rs].sum += (tr[rs].r - tr[rs].l + 1) * tr[k].tag;
    tr[k].tag = 0;
}

然后我们在更新一下查询和修改的函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
void update(int k, int l, int r, int v)
{
    if(l <= tr[k].l && tr[k].r <= r)
    {
        tr[k].sum += (tr[k].r - tr[k].l + 1) * v;
        tr[k].tag += v;
        return;
    }
    pushdown(k);
    int mid = (tr[k].l + tr[k].r) >> 1;
    if(l <= mid) update(ls, l, r, v);
    if(r > mid) update(rs, l, r, v);
    pushup(k);
}

int query(int k, int l, int r)
{
    int res = 0;
    if(l <= tr[k].l && tr[k].r <= r)
    {
        return tr[k].sum;
    }
    pushdown(k);
    int mid = (tr[k].l + tr[k].r) >> 1;
    if(l <= mid) res += query(ls, l, r);
    if(r > mid) res += query(rs, l, r);
    return res;
}

线段树提高

目前我们已经解决了线段树维护区间和的问题。线段树维护区间极值也很简单，只需要在原来的代码上稍作修改即可。但是，作为十分美丽的数据结构，线段树可以维护的东西远不止这些。接下来让我们看看线段树更为进阶的用法。

维护区间平方和

给定序列 \(\{a_n\}\)，\(q\) 次操作，每次操作诸如：

1 l r v：给区间 \([l,r]\) 的每个元素加上 \(v\)；

2 l r：查询区间 \([l,r]\) 的平方和，即 \(\sum\limits_{i=l}^{r}a_i^2\)。

\(1\leq n,q\leq 10^5\)。

这时候就需要我们思考，线段树要维护某些东西具体需要改什么。

原本有一段需要修改的区间 \(a_l, a_{l+1}, ..., a_r\)。我们需要维护的东西是 \(\sum\limits_{i=l}^{r}a_i^2\)。

考虑我们现在对这段东西整体加上 \(v\)，那么我们的答案就变成了 \(\sum\limits_{i=l}^{r}(a_i+v)^2\)。

运用我们初中就学过的完全平方公式：

\(\sum\limits_{i=l}^{r}(a_i+v)^2 = \sum\limits_{i=l}^{r}(a_i^2+2a_iv+v^2) = \sum\limits_{i=l}^{r}a_i^2+2v\sum\limits_{i=l}^{r}a_i+(r-l+1)v^2\)

我们发现前面的 \(\sum\limits_{i=l}^{r}a_i^2\) 就是我们原先的值，而最后的 \((r-l+1)v^2\) 可以直接算出来，中间的 \(2v\sum\limits_{i=l}^{r}a_i\) 只需要多维护一个区间和就可以了。

那么，这道题我们就需要维护两个值：区间平方和、区间和。修改的时候按照公式中的修改即可。

思考：区间方差。

给定序列 \(\{a_n\}\)，\(q\) 次操作，每次操作诸如：

1 l r v：给区间 \([l,r]\) 的每个元素加上 \(v\)；

2 l r：查询区间 \([l,r]\) 的方差。

方差：\(\sigma^2=\dfrac{1}{n}\sum\limits_{i=1}^{n}(x_i-\overline x)^2\)

\(1\leq n,q\leq 10^5\)。

区间乘与区间加

给定序列 \(\{a_n\}\)，\(q\) 次操作，每次操作诸如：

1 l r v：给区间 \([l,r]\) 的每个元素加上 \(v\)；

2 l r v：给区间 \([l,r]\) 的每个元素乘上 \(v\)；

3 l r：查询区间 \([l,r]\) 的和。

\(1\leq n,q\leq 10^5\)。

这不好做？我直接开两个 \(tag\)，分别维护加法和乘法懒标记，结果一合并不就行了！

等等，你先别急。你乘法和加法分别统计真的对吗？

例如，我们当前的数是 \(2\)，对当前的数分别 \(\times 3,+2,\times 4\)，答案应当是 \((2\times 3+2)\times 4=32\)。但是如果我们分别计算 \(multitag=3\times 4=12,plustag=2\)，答案就会变成 \(2\times12+2=26\) 或者 \((2+2)\times 12=48\)。

这是因为我们加法和乘法之间是有运算顺序的，因此我们不能简单地直接计算。

那有没有什么办法呢？当然有！我们在小学就学过一个伟大的东西，叫做乘法的分配律！

假设我们当前的节点有 \(multitag\) 和 \(plustag\) 两个 \(tag\)，那么当前节点的值应当是 \((x\times multitag+plustag)\)，现在对这个节点进行 \(\times v\) 的操作就会变成 \((x\times multitag+plustag)\times v=x\times multitag\times v + plustag\times v\)。

于是，我们正常维护 \(multitag\)，并且额外更新 \(plustag\)，这样就可以了。

区间开根

给定序列 \(\{a_n\}\)，\(q\) 次操作，每次操作诸如：

1 l r v：令区间 \([l,r]\) 的每个元素 \(x\) 变成 \(\lfloor\sqrt{x}\rfloor\)；

2 l r：查询区间 \([l,r]\) 的和。

\(1\leq n,q\leq 10^5,1\leq a_i\leq 10^{18}\)。

有没有发现这次的题目多了一个数据范围？

既然 \(a_i\leq 10^{18}\)，我们发现至多进行 \(6\) 次 \(1\) 操作，当前的数就会变成 \(1\)。变成 \(1\) 之后自然之后的操作都是无效的操作。

那么，我们在更改的时候可以暴力更改当前区间的数，并记录当前区间的最大值。如果最大值小于等于 \(1\)，那么就可以停止这个区间的更改了。

这样，查询的复杂度是不变的单次 \(O(\log n)\)，我们来分析一下修改的时间复杂度。

不将值域局限在 \(10^{18}\) 内，我们考虑一个数会被更改多少次：

\(a^{\left(\frac{1}{2}\right)^x}<2\)。

这是一个两层不等式，想得到 \(x\) 我们需要取两次对数，因此我们每个数最多会被更改 \(O(\log\log a)\) （\(a\) 为 \(a_i\) 的最大值）次。考虑我们暴力更改就相当于是单点修改，那么每对一个元素修改的复杂度就是 \(O(\log n)\) 的。我们一共有 \(n\) 个元素，每个元素修改一次的复杂度是 \(O(\log n)\)，每个元素最多会被更改 \(O(\log\log a)\) 次，那么，总的时间复杂度就是 \(O(n\log n\log\log a)\)。单次的复杂度均摊是 \(O(\log n\log\log a)\) 的。可以通过本题。

维护前前缀和

前缀和：\(S_i=\sum\limits_{k=1}^{i}a_k\)；

前前缀和：\(SS_i=\sum\limits_{k=1}^{i}S_i\)。

给定序列 \(\{a_n\}\)，\(q\) 次操作，每次操作诸如：

1 x v：将 \(a_x\) 加上 \(v\)；

2 x：查询 \(SS_x\)。

\(1\leq n,q\leq 10^5\)。

我们现在有三个数组：原数组 \(a\)，前缀和数组 \(S\)，前前缀和数组 \(SS\)。

对于 \(1\) 操作，我们要用到的是 \(a\)。对于 \(2\) 操作，我们要用到的是 \(SS\)。那么，我们为什么不选择一个中间商赚个差价方便我们对两边都能维护到呢？

因此，我们可以维护前缀和数组 \(S\)，对于操作 \(2\)，答案即是从 \(1\) 开始的区间和。对于操作 \(1\)，我们只需要让从当前位置开始到 \(n\) 的区间加上 \(v\) 即可。

区间加等差数列

给定序列 \(\{a_n\}\)，\(q\) 次操作，每次操作诸如： 1 l r d k：令区间 \([l,r]\) 的每个元素 \(a_i\) 加上以 \(d\) 为首项、\(k\) 为公差的等差数列 \(\{c\}\) 的 \(c_i\)。 2 l r：查询区间 \([l,r]\) 的和。 \(1\leq n,q\leq 10^5\)。

区间加的数不是同一个数，怎么办？

考虑一下等差数列的性质。我们没有必要知道每一个数是什么，我们只需要知道首项和公差，就可以推出数列的任意一项以及数列的和。那我们不妨用线段树维护加的等差数列的首项和公差。

维护区间最大子段和

给定序列 \(\{a_n\}\)，\(q\) 次操作，每次操作诸如：

1 x v：将 \(a_x\) 加上 \(v\)；

2 l r：查询区间 \([l,r]\) 内的最大子段和。

\(1\leq n,q\leq 10^5\)。

这咋做？

线段树保证复杂度的关键一步是要保证可以快速、正确地合并。这题单点修改是容易的，关键在于如何让信息快速合并。

我们思考一下合并区间最大子段和时，可能有哪些情况：

  1. 全部在左半区间。
  2. 全部在右半区间。
  3. 横跨左右区间。

我们显然是要维护当前区间的最大子段和的。对于 \(1\) 情况和 \(2\) 情况，直接合并就可以了。关键是 \(3\) 情况该如何合并。

我们考虑横跨左右区间实际上就是左半区间右端点开始的区间最大子段和，和右半区间左端点开始的区间最大子段和合并。那我们不妨对每个节点多维护两个信息：以右端点开始的区间最大子段和（记作 \(S[k]_r\)），和以左端点开始的区间最大子段和（记作 \(S[k]_l\)）。这样，我们就可以做到快速算出区间最大子段和了。

不过问题在于，我们新维护的这两个值也需要考虑合并之后该怎么办。只考虑 \(S[k]_l\)，这个时候有两种情况：

  1. \(S[k]_l\) 是 \(S[ls(k)]_l\)。
  2. \(S[k]_l\) 的右端点跨到了右区间，答案变成 \(sum_k+S[rs]_l\)。

而且只有这两种情况。（思考一下，为什么？）

现在所有问题已经解决，我们就可以快速维护了。

思考：\(1\) 操作改为区间加怎么做？

信息的本质

我们发现，线段树可以维护许多东西：区间和、区间极值……通过一些手法，我们也可以维护诸如区间最大子段和的东西。

那么，究竟什么样的信息才可以被维护呢？

首先，这个信息必须是可被快速合并的。其次，这个信息必须满足结合律。因为我们在合并的时候其实是并不关心信息之间的顺序的，这就要求其必须满足结合律。那么可以看出，这些信息实际上构成了一个半群。

以上情况都是在单点修改的时候。那么区间修改呢？为什么刚刚线段树维护区间最大子段和没办法区间修改呢？

在区间修改的时候，为了保证线段树复杂度的正确性，我们势必要引入标记。那么，这个标记也必须满足一定的性质。

首先，这个标记必须是可被快速合并的。其次，这个标记必须满足结合律。第三，这个标记必须可被快速作用到信息上。可以看出，标记实际上构成了一个幺半群。

因此，我们在考虑线段树维护某些东西的时候，一方面要考虑如何维护信息，另一方面要考虑如何维护标记。

有关更多这部分的内容，可以看_rqy的博客。

线段树的本质

不同的人对线段树有不同的理解，这里分享一些我的个人看法。

所谓线段树，实际上是针对原来的序列，递归地建立新结点，维护若干个原来节点的信息，当询问时，我们就可以直接采用某些节点的信息，以达到快速查询的目的。

照这么说，我们其实还可以写出 \(3\) 叉线段树、\(4\) 叉线段树、\(\sqrt{n}\) 叉线段树……

\(\sqrt{n}\) 叉？分块？

很相类似。狭义上的数据结构本质上都是对序列进行划分，线段树是划分为 \(O(\log n)\) 个区间，分块则是分成 \(O(\sqrt{n})\) 个区间。

不过线段树和分块仍有一些本质上的区别：线段树对于数据，更倾向形成一种树状结构，而分块更倾向于形成线性结构。

线段树的常用技巧

动态开点

有的时候，面对庞大的数据范围，我们没办法开如此大的空间。这个时候，我们就需要动态开点线段树了。

动态开点线段树，顾名思义，即对于整颗线段树，我们并不将它直接建出来，而是到用到某个节点了在进行新建。

因此，我们就直接不建树，在 update 和 query 的时候，如果当前没有节点，那么我们就新建一个。

不过，显然此时我们再沿用之前 \(2k\) 为左儿子编号，\(2k+1\) 为右儿子编号的做法不再合适。我们需要额外记录当前节点左右儿子的编号。

考虑到一次操作最多会访问 \(O(\log n)\) 个节点，那么总空间复杂度为 \(O(q\log n)\)。

考虑到一颗线段树的节点数是 \(2n-1\)，因此动态开点时只需开 \(2\) 倍空间即可。

因此我们只需要对应更改一下 pushdown 和 update 的代码即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
struct Seg_Tree
{
    int sum, tag;
    int lson, rson;
}tr[MAXN << 1];

void f(int &k, int l, int r, int v)
{
    if(!k) k = ++cnt;
    tr[k].tag += v;
    tr[k].sum += v * (r - l + 1);
}

void pushdown(int k, int l, int r)
{
    int mid = l + r >> 1;
    f(ls, l, mid, tr[k].tag);
    f(rs, mid + 1, r, tr[k].tag);
    tr[k].tag = 0;
}

void update(int &k, int l, int r, int L, int R, int v)
{
    if(L <= l && r <= R) return f(k, l, r, v);
    pushdown(k, l, r);
    int mid = l + r >> 1;
    if(L <= mid) update(ls, l, mid, L, R, v);
    if(R > mid) update(rs, mid+ 1, r, L, R, v);
    pushup(k);
}

我们初始时需要建立第一个节点。值得注意的是：update 和 f 函数中的 \(k\) 必须加取地址符，这是为了使儿子信息在父亲节点中被更新。

标记永久化

当数据范围较大、或者 pushdown、pushup 代价过高时，可以考虑标记永久化。

我们知道线段树一个重要的部分是懒标记，而 pushdown 就是为了下放标记而存在的。而标记永久化则是不进行标记的下放，直接永久记录在该节点上。当我们需要访问某节点时，叠加所有在它到根节点路径的标记即可。

然而值得注意的是，并不是所有的标记都能永久化。除了要满足标记本身需要满足的条件之外，还需要满足交换律。

标记永久化并没有时空复杂度的提升，但是可以优化时间常数。某些情况下，标记下放可能会比较麻烦，这时使用标记永久化不失为一个好的选择。

标记永久化可以保证了当前节点子树的更新，但是与之相对的，当前节点到根我们需要额外维护：从根到该节点，每次取当前节点维护区间与修改区间的交集，进行更新。

下面是动态开点+标记永久化的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void update(int &k, int l, int r, int L, int R, int v)
{
    if(!k) k = ++cnt;
    if(L <= l && r <= R) return (void)(tr[k].tag += v);
    tr[k].sum += v * (min(R, r) - max(L, l) + 1);
    int mid = l + r >> 1;
    if(L <= mid) update(ls, l, mid, L, R, v);
    if(R > mid) update(rs, mid + 1, r, L, R, v);
}

int query(int k, int l, int r, int L, int R)
{
    if(!k) return 0;
    if(L <= l && r <= R) return tr[k].sum +(r - l + 1) * tr[k].tag;
    int res = (min(R, r) - max(L, l) + 1) * tr[k].tag;
    int mid = l + r >> 1;
    if(L <= mid) res += query(ls, l, mid, L, R);
    if(R > mid) res += query(rs, mid + 1, r , L, R);
    return res;
}

线段树二分

线段树本身看起来就是个很二分的结构。那么我们不妨直接利用这个结构特性来进行二分。

类比于我们在线段树基本操作中的单点修改，我们发现这个其实就是一个不断二分的过程。

这样的时间复杂度可以维持在 \(O(\log n)\)。

线段树进阶

值域线段树

还是先来看一个问题：

给定序列 \(\{a_n\}\)，\(q\) 次询问。

每次询问给定 \(k\)，求序列第 \(k\) 小。

\(1\leq n,q\leq 10^5,1\leq a_i\leq 10^9\)。

想要解决这个问题，我们需要用到“值域线段树”。

值域线段树，也被称作“权值线段树”，但是值域线段树这个名字更加严谨一点。

佛说：诞生了数组之后，就诞生了桶。同样，诞生了线段树之后，就诞生了值域线段树。

具体来说，值域线段树也是一种线段树，但是它维护的范围从 \(n\) 变成了整个值域（因此需要动态开点），而维护的东西则是一段区间内数的出现次数。形象化地说，就是在桶上建立了一颗线段树。

那么想想如何查询第 \(k\) 小。通过刚才线段树二分的思想，我们每次将当前节点左右儿子的值与 \(k\) 比较，然后二分地寻找应该存在的地方。

值域线段树

如图，对于序列 \(\{1,2,3,4,2,3,4,3,4,4\}\)，我们可以建立如上值域线段树。例如我们现在要查询 \(k=5\)，红色的节点和边就是我们查询的路径。值得注意的是，我们的 \(k\) 应该是在当前节点区间内的 \(k\)，这意味着如果我们递归到了右子树，需要减去左子树的值。

类似地，值域线段树也支持单点修改，以及查询某个数出现个数等等。

注意到，普通值域线段树只支持全局查询。若需要区间查询，则需要对值域线段树进行可持久化，即主席树。

扫描线

具体来说，扫描线是一种思想，而不是一种数据结构。

扫描线比较经典的问题就是求矩形面积并了。

给定若干四边平行于坐标轴的矩形。

求它们的面积并（重合部分只算一次）。

\(n\leq 10^5,|x_i|,|y_i|\leq 10^9\)。

线段树维护矩形面积并

扫描线

如上图所示，我们将蓝绿两个矩形通过虚线分割成了三块。显然，答案应该是三段的线段长度 \(len\) 分别乘上这段竖着的长度之和 \(sum\)。

前者我们已经知道了，我们只需要快速维护后者即可。可以用线段树维护。

具体来说，我们通过一根红色的“扫描线”从下向上扫。记矩形的下边界为 \(+1\)，上边界为 \(-1\)，同时维护 \(sum\) 即可。

由于范围很大，因此需要离散化。如果你不想离散化，还可以使用动态开点+标记永久化，代码会更短。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void pushup(int k, int l, int r)
{
    if(tr[k].tag) tr[k].sum = r - l + 1;
    else tr[k].sum = tr[ls].sum + tr[rs].sum;
}

void update(int &k, int l, int r, int L, int R, int v)
{
    if(!k) k = ++cnt;
    if(L <= l && r <= R) return (void)(tr[k].tag += v, pushup(k, l, r));
    int mid = l + r >> 1;
    if(L <= mid) update(ls, l, mid, L, R, v);
    if(R > mid) update(rs, mid + 1, r, L, R, v);
    pushup(k, l, r);
}

本质

我们来思考一下扫描线的本质：考虑一下我们刚才引入的这条“扫描线”在干什么？在枚举。而我们为了达到同时枚举 \(x,y\) 的目的，在扫描 \(y\) 的同时，快速更新 \(x\) 的贡献。这就是扫描线思想。

也就是说，对于 \((x,y)\) 的枚举，我们可以枚举其中一维，并同时通过数据结构快速维护另一维，以求出答案。

李超线段树

要求在平面直角坐标系下维护两个操作：

  1. 在平面上加入一条线段。记第 \(i\) 条被插入的线段的标号为 \(i\)；

  2. 给定一个数 \(k\)，询问与直线 \(x = k\) 相交的线段中，交点纵坐标最大的线段的最小编号。

强制在线。\(n\leq 10^5\)。

这个问题普通线段树无法解决，这个时候，李超线段树就派上用场了。李超树由浙江学军中学的李超发明，用于维护这样一类普通线段树无法维护的问题。

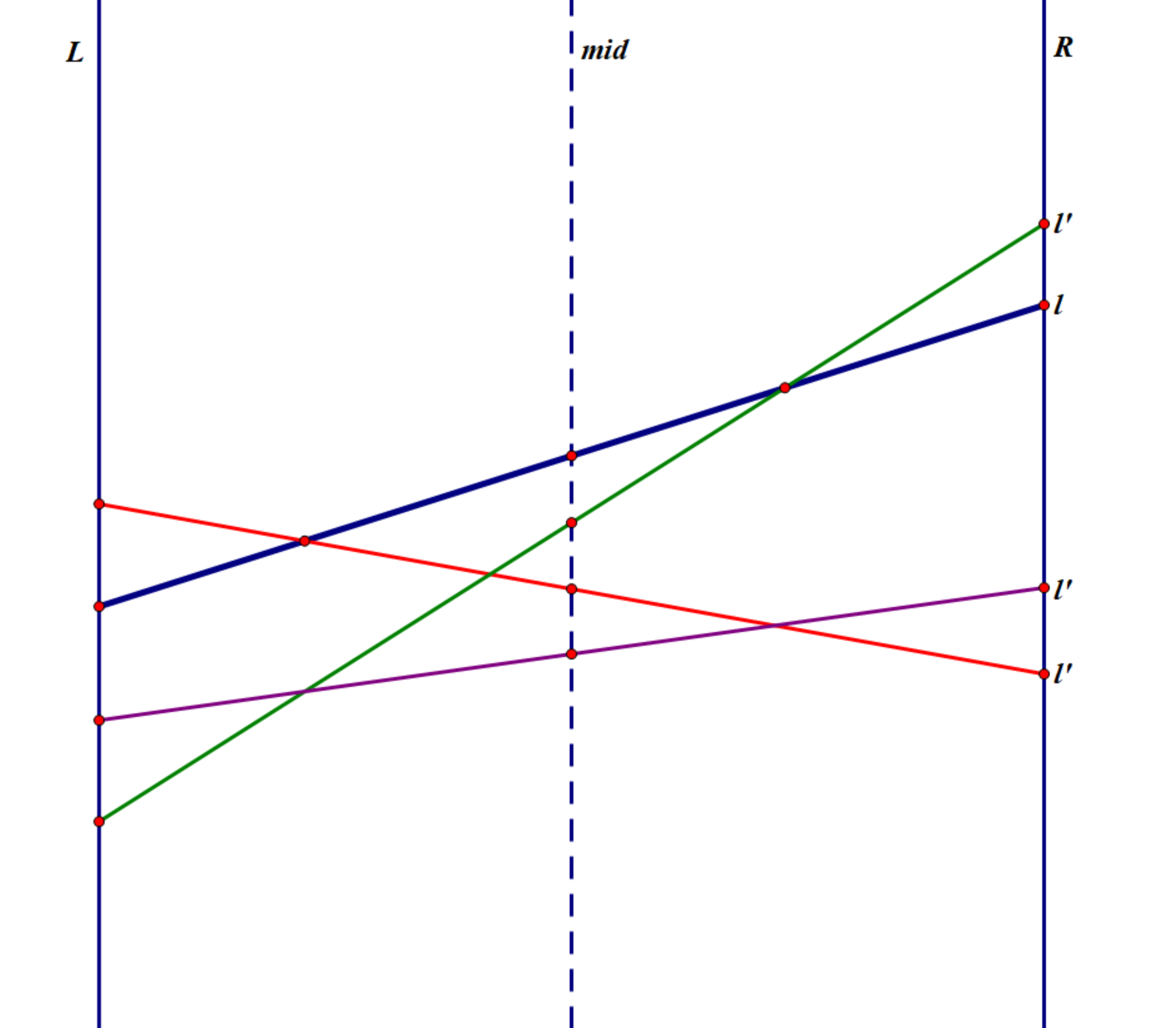
李超线段树维护 \(x=mid\) 时最大的线段信息。记我们现在的最优线段为 \(l\)，新加入的线段（完全覆盖此区间）为 \(l'\)。那么，我们将 \(l\) 与 \(l'\) 比较，若 \(l'\) 在 \(mid\) 处更优，则交换 \(l\) 与 \(l'\)。

接下来，对于 \(l'\) 在 \(mid\) 处不比 \(l\) 优的情况，有下列几种：

  1. 在左端点 \(l'\) 优于 \(l\)，则一定在左区间中产生交点，递归左子树。
  2. 在右端点 \(l'\) 优于 \(l\)，则一定在右区间中产生交点，递归右子树。
  3. 在左右端点均不优，则不需要修改。
李超线段树

如上图，蓝线是我们的原来最优线段 \(l\)，红线、绿线、紫线依次表示三种情况。

以红线为例：在 \(L\) 时，\(l'_L>l_L\)，说明 \(l\) 和 \(l'\) 一定在 \([L,mid]\) 有交点，那么我们就递归 \([L,mid]\) 的区间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
int cmp(double x, double y)
{
    if(x - y > eps) return 1;
    if(y - x > eps) return -1;
    return 0;
}

double calc(int k, int dis){return a[k].b + a[k].k * dis;}

void modify(int k, int l, int r, int u)
{
    int &v = tr[k], mid = l + r >> 1;
    int xmid = cmp(calc(u, mid), calc(v, mid));
    if(xmid == 1 || (!xmid && u < v)) swap(u, v);
    int xl = cmp(calc(u, l), calc(v, l)), xr = cmp(calc(u, r), calc(v, r));
    if(xl == 1 || (!xl && u < v)) modify(ls, l, mid, u);
    if(xr == 1 || (!xr && u < v)) modify(rs, mid + 1, r, u);
}

void update(int k, int l, int r, int L, int R, int u)
{
    if(L <= l && r <= R) return (void)modify(k, l, r, u);
    int mid = l + r >> 1;
    if(L <= mid) update(ls, l, mid, L, R, u);
    if(R > mid) update(rs, mid + 1, r, L, R, u);
}

查询 \(x\) 时，从根节点走到 \([x,x]\) 的所有最优线段在 \(x\) 处的极值即为答案，类似于标记永久化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
pdi pmax(pdi x, pdi y)
{
    if(cmp(x.fi, y.fi) == 1) return x;
    else if(cmp(x.fi, y.fi) == -1) return y;
    else return x.se < y.se ? x : y;
}

pdi query(int k, int l, int r, int x)
{
    if(l > x || x > r) return {0, 0};
    int mid = l + r >> 1;
    double res = calc(tr[k], x);
    if(l == r) return {res, tr[k]};
    return pmax({res, tr[k]}, pmax(query(ls, l, mid, x), query(rs, mid + 1, r, x)));
}

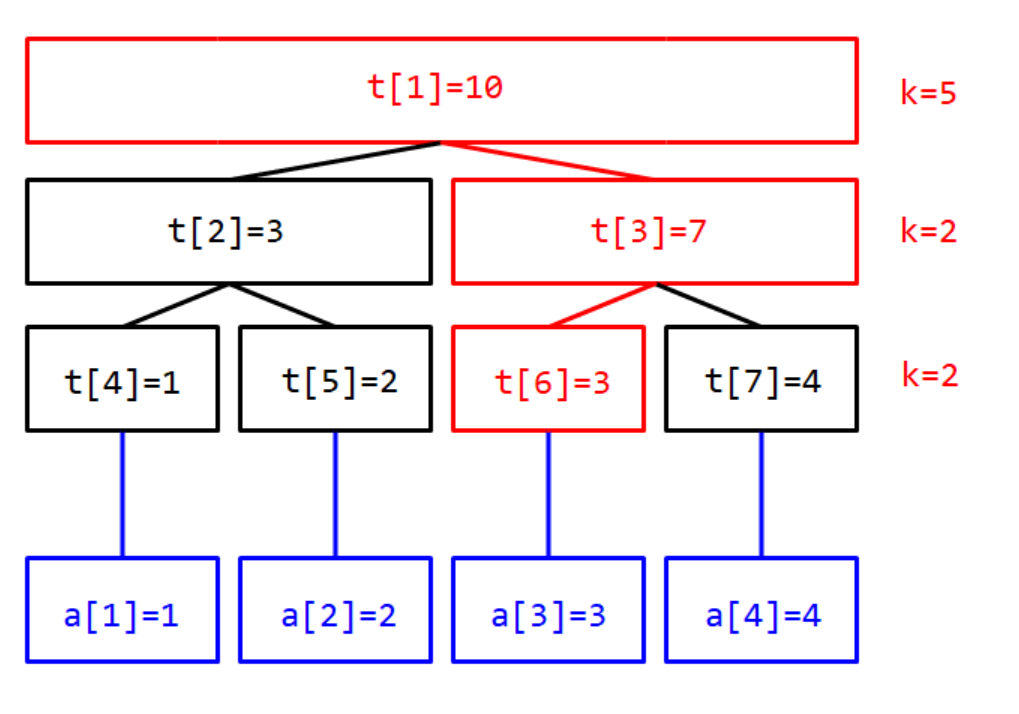
zkw 线段树

zkw 线段树，即非递归式线段树，由张昆玮发明的一种更加快速、方便、易写的线段树。

结构

我们将线段树开成满二叉树。容易发现这样一些性质：

  1. 记当前节点编号为 \(k\)，则左儿子编号为 \(k<<1\)，右儿子编号为 \(k<<1|1\)。反之，父亲节点编号为 \(k>>1\)。
  2. 前 \(n\) 层节点数为 \(2^n-1\)，第 \(n\) 层节点数为 \(2^{n-1}\)。
  3. 叶子是一段连续的编号，且与原序列可一一对应。

一反之前线段树自上向下递归的方式，zkw 线段树一般采用从叶子向根节点的非递归方式。

建树

根据刚才的性质，我们只需要把原序列填到这段叶子序列上即可。第一个叶子节点的编号可以 \(O(\log n)\) 地求出。

1
2
3
4
5
6
void build()
{
    for(N = 1; N <= n + 1; N <<= 1);
    for(int i = 1; i <= n; i++) tr[N + i] = a[i];
    for(int i = N - 1; i >= 1; i--) tr[i] = tr[i << 1] + tr[i << 1 | 1];
}

其中，\(N\) 为非叶子结点的个数。

单点修改、区间查询

很简单，我们只需要找到对应的叶子节点，一路走到根节点修改即可。

1
2
3
4
void update(int k, int v)
{
    for(k += N; k; k >>= 1) tr[k] += v;
}

实际代码写起来只有一行，非常简短。

接下来思考区间查询。从叶子节点向上，我们怎么实现区间查询呢？

这里有一个非常巧妙的思想：从我们当前要查询的叶子区间的左右两个节点分别记一个 \(l,r\) 值，然后不断向父亲节点跳，直到其父亲节点为同一个点为止。

在跳的过程中，若 \(l\) 为左儿子，则计算右儿子的贡献；若 \(r\) 为右儿子，则记录左儿子的贡献。

简单证明一下这么做的正确性：

会被计算贡献的只有 \((l,r)\) 的部分。在向上跳的过程中，\((l,r)\) 间显然不会出现不被计算的情况。\(l\) 若为左儿子，则其兄弟节点一定在 \((l,r)\) 中，否则其右侧的点一定会被上一层计算到。而线段树需要计算的节点显然只会在最两边，因此这样计算是正确的。

那么我们可以写出如下代码：

1
2
3
4
5
6
7
8
9
10
int query(int k, int l, int r)
{
    int ans = 0;
    for(l = N + l - 1, r = N + r + 1; l ^ r ^ 1; l >>= 1, r >>= 1)
    {
        if(~l & 1) ans += tr[l ^ 1];
        if(r & 1) ans += tr[r ^ 1];
    }
    return ans;
}

其中用到的位运算：

  1. l ^ r ^ 1：若 \(l,r\) 互为兄弟，则一定为 \(2k\) 与 \(2k+1\)，其异或值 \(1\)。
  2. l >>= 1：跳父节点。r >>= 1 同理。
  3. ~l & 1：若 \(l\) 为左儿子，则末尾为 \(0\)，否则为 \(1\)，将末尾取反后再按位与 \(1\) 即可判断是否为左儿子。r & 1 同理。

区间修改、区间查询

区间修改，就势必要打标记。如果我们不能下放标记，那该怎么办呢？

标记永久化！

因此区间修改、区间查询的代码可以这么写：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void update(int l, int r, int v)
{
    int numl = 0, numr = 0, num = 1;
    for(l = N + l - 1, r = N + r + 1; l ^ r ^ 1; l >>= 1, r >>= 1, num <<= 1)
    {
        tr[l] += v * numl, tr[r] += v * numr;
        if(~l & 1) tag[l ^ 1] += v, tr[l ^ 1] += v * num, numl += num;
        if(r & 1) tag[r ^ 1] += v, tr[r ^ 1] += v * num, numr += num;
    }
    for(; l; l >>= 1, r >>= 1) tr[l] += v * numl, tr[r] += v * numr;
}

int query(int l, int r)
{
    int numl = 0, numr = 0, num = 1, ans = 0;
    for(l = N + l - 1, r = N + r + 1; l ^ r ^ 1; l >>= 1, r >>= 1, num <<= 1)
    {
        if(tag[l]) ans += tag[l] * numl;
        if(tag[r]) ans += tag[r] * numr;
        if(~l & 1) ans += tr[l ^ 1], numl += num;
        if(r & 1) ans += tr[r ^ 1], numr += num;
    }
    for(; l; l >>= 1, r >>= 1) ans += tag[l] * numl, ans += tag[r] * numr;
    return ans;
}

多线段树操作

线段树合并

线段树合并，顾名思义，将两颗线段树合并为一颗新的线段树。

线段树合并其实极为暴力。一般来说，对于两颗动态开点的值域线段树，我们可以从 \(1\) 开始递归合并。若当前节点一颗为空，另一颗不为空，则直接返回不为空的节点。若递归到叶子节点，直接合并。最后更新即可。

时间复杂度为 \(O(n\log n)\)。

例如，对于将两颗值域线段树按加法合并，可以这么写：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#define ls(k) tr[k].lson
#define rs(k) tr[k].rson

int merge(int a, int b, int l, int r)
{
    if(!a || !b) return a + b;
    if(l == r)
    {
        tr[a].val += t[b].val;
        return a;
    }
    int mid = l + r >> 1;
    ls(a) = merge(ls(a), ls(b), l, mid);
    rs(a) = merge(rs(a), rs(b), mid + 1, r);
    pushup(a);
    return a;
}

当然，你也可以选择新开一颗线段树合并进去。优点是不会破坏原来线段树的结构，缺点是需要较大的空间。

线段树分裂

线段树分裂是线段树合并的逆操作。

类似于 FHQ-Treap。先挖个坑。

主席树

简介

主席树，全称可持久化值域线段树，因其发明者黄嘉泰名字首字母与某位历史上的主席相同，因此称为主席树。

主席树一般用于解决静态区间第 \(k\) 小问题。

结构

如果是全局第 \(k\) 小问题，那么我们显然可以用值域线段树完成。

值域线段树维护的是区间内数字出现次数。这个是一个可减信息。那么运用前缀和的思想，我们分别建立出维护区间 \([1,i]\) 的值域线段树 \(T_i\)，最后将查询到的信息相减不就好了？

等等。一颗线段树的空间复杂度就是 \(O(n\log n)\) 的了，建 \(n\) 颗岂不是炸飞了？

我们考虑能否在建立 \(T_i\) 的时候充分利用 \(T_{i-1}\) 的信息。由于 \(T_{i-1}\rightarrow T_i\) 实际上相当于单点修改，因此我们只会影响到 \(O(\log n)\) 个节点，只需要把这 \(O(\log n)\) 个节点多开出来就可以了。

主席树

过于抽象？来看张图。

在这张图中，黑色节点与蓝色节点共同构成了 \(T_{i-1}\)，黑色节点与红色节点共同构成了 \(T_i\)。一条红色箭头代表了该蓝色节点被影响后，重建出来的红色节点。如果我们忽视所有的虚线，那么得到的就是新线段树。

如果你的空间想象能力足够强大，那么你可以这么理解：线段树通常被画为二维平面的图像。而不同的版本意味着我们再引入一条垂直于平面的坐标轴“版本轴”，或者“时间轴”。对于影响到的节点，我们直接在新的版本平面内建立出来，而对于还可以利用的节点，我们连接向上一个版本平面的节点。

立体主席树1
立体主席树2

操作

查询的时候，我们在两颗线段树上分别查询就可以了，这个没有太大的问题。同样，单点修改也没有太大的问题。

那么，我们可以写出如下代码；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
struct Node
{
    int lson, rson;
    int val;
}tr[MAXN << 5];

int rt[MAXN << 5], cnt; //rt 表示每个版本的根

void build(int &k, int l, int r)
{
    if(!k) k = ++cnt;
    if(l == r) return;
    int mid = l + r >> 1;
    build(ls(k), l, mid);
    build(rs(k), mid + 1, r);
}

int update(int k, int l, int r, int v)
{
    int nk = ++cnt;
    tr[nk] = tr[k], tr[nk].val++; //建立新的节点
    if(l == r) return nk;
    int mid = l + r >> 1;
    if(v <= mid) ls(nk) = update(ls(nk), l, mid, v);
    else rs(nk) = update(rs(nk), mid + 1, r, v);
    return nk;
}

//x,y 分别表示两个版本的根节点
int query(int x, int y, int l, int r, int v)
{
    if(l == r) return l;
    int mid = l + r >> 1;
    int num = tr[ls(y)].val - tr[ls(x)].val;
    if(num >= v) return query(ls(x), ls(y), l, mid, v);
    else return query(rs(x), rs(y), mid + 1, r, v - num);
}

区间修改

对于一颗普通的可持久化线段树，如果我们要区间修改，貌似还有些麻烦。

保证线段树复杂度正确性的一个重要部分是懒惰标记 \(tag\)。但是当一个节点被多个版本的父亲公用，就出现了问题：如果我们直接将标记打到儿子节点，那么多个版本就会受到影响，正确性是错的。

面对这种问题，一般有两种方法：

第一种：在 pushdown 的时候，如果要下放的节点不在当前版本，那就在当前版本新建节点。由于每次至多新建两个节点，因此时间复杂度仍然是 \(O(\log n)\)；

第二种：运用标记永久化的思想，不进行标记下放。

一般来说，第二种更加方便、好写，但也有部分无法处理的情况。如果使用第一种方法，则 update 和 query 时都要 pushdown 新建节点。

至此，线段树基本内容已经处理完毕。

线段树再进阶

吉司机线段树

吉司机线段树（Segment Tree Beats!）。

我不会。

Kinetic Tournament Tree

势能竞赛树（我瞎翻译的），简称 KTT，是一类求解下述特殊问题的线段树变种：

给定 \(\mathbb{R}\rightarrow\mathbb{R}\) 上的一次函数序列 \(\{f_n\},f_i=k_ix+b_i\)，以及一个自变量序列 \(\{x_n\}\)，有以下两种操作：

  1. 给定 \(l,r,v\)，\(\forall i\in[l,r],x_i\leftarrow x_i+v\)；

  2. 给定 \(l,r\)，求 \(\max\limits_{i=l}^{r}f_{i}(x_i)\)。

KTT 以这样的方式解决上述问题：

维护一颗线段树，每个节点维护取到 \(\max f_i(x_i)\) 的 \(f_i\)，即对应自变量下，函数值最大的函数，称其为区间最优函数。同时记录一个阈值 \(th\)，表示当该区间 \(x_i\leftarrow x_i+v\) 后，区间最优函数发生改变的最小 \(v\) 值，称其为区间最优函数的最近切换点。

区间修改时，若 \(v< th\)，则直接操作即可；否则继续递归，暴力修改左右子树。

上传信息时，除了要上传原本的信息，还要计算阈值的最小值。

时间复杂度分析详见 2020 国家集训队论文《浅谈函数最值的动态维护》，为 \(O(n\log^2 n+m\log^3 n+q\log n)\)，其中 \(m,q\) 分别为 \(1,2\) 操作的次数。

例题。

题目随解

k-Maximum Subsequence Sum

CF280D k-Maximum Subsequence Sum

在给定序列 \(\{a_n\}\) 中选取不超过 \(k\) 段不相交的区间 \([l_i, r_i](l_i\leq r_i)\)，使 \(\sum\limits_{i=1}^{k}\sum\limits_{j=l_i}^{r_i}a_{j}\) 最大。

需要支持单点覆盖。

\(1\leq n,q\leq 10^5,k\leq 20\)。

当 \(k=1\) 时，题目变为区间最大子段和。这个问题我们在上面已经学过。

那么 \(k>1\) 的时候呢？考虑一个贪心：每次选取当前最大子段和，并将其 \(\times -1\)，重复 \(k\) 次，然后取 \(1\sim k\) 中的最大值。

这个贪心的正确性可以用费用流证明：\(S\rightarrow i,i\rightarrow T\) 连一条流量为 \(1\)，费用为 \(0\) 的边，\(i\rightarrow i+1\) 连一条流量为 \(1\)，费用为 \(a_i\) 的边。那么一条 \(S\rightarrow i\rightarrow j \rightarrow T\) 的流表示选择了 \([i,j-1]\)。之后引入反流，每次将前一项 \(\times -1\)，新区间 \([l,r]\) 与旧区间 \([x,y]\) 若有交集，则说明 \([x,y]\) 有一部分被反悔。显然，\([l,r]\) 与 \([x,y]\) 不可能存在包含关系。因此 \(k\) 轮增广之后，我们就得到了答案。

考虑要维护什么：区间最大子段和的必须品区间和 \(sum\)，左端点开始的最大子段和 \(lft\)，右端点开始的最大子段和 \(rgt\)，区间最大子段和最 \(ans\)。由于要取反，我们还要维护一个左端点开始的最小子段和，右端点开始的最小子段和，区间最小子段和。可以分别用两个结构体封装，方便以后的操作。由于我们要记录反转哪里，所以还需要分别维护最大最小的子段和左端点 \(ansl\)、右端点 \(ansr\)，左端点开始的子段和右端点 \(lftr\)，右端点开始的子段和左端点 \(rgtl\)，以及一个翻转标记 \(tag\)。

Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
struct sub
{
    int ans, lft, rgt;
    int ansl, ansr, lftr, rgtl;
    void init(int x, int i){ans = lft = rgt = x; if(i != -1) ansl = ansr = lftr = rgtl = i;};
    void mul_1(){ans *= -1, lft *= -1, rgt *= -1;}
};

struct Node
{
    int sum;
    sub big, sml;
    int tag;
}tr[MAXN << 2];

void pushup(int k)
{
    tr[k].sum = tr[ls].sum + tr[rs].sum;
    //以上为区间和
    if(tr[ls].big.ans > tr[rs].big.ans) tr[k].big.ans = tr[ls].big.ans, tr[k].big.ansl = tr[ls].big.ansl, tr[k].big.ansr = tr[ls].big.ansr;
    else tr[k].big.ans = tr[rs].big.ans, tr[k].big.ansl = tr[rs].big.ansl, tr[k].big.ansr = tr[rs].big.ansr;
    if(tr[ls].big.rgt + tr[rs].big.lft > tr[k].big.ans) tr[k].big.ans = tr[ls].big.rgt + tr[rs].big.lft, tr[k].big.ansl = tr[ls].big.rgtl, tr[k].big.ansr = tr[rs].big.lftr;
    //以上为区间最大子段和
    if(tr[ls].sum + tr[rs].big.lft > tr[ls].big.lft) tr[k].big.lft = tr[ls].sum + tr[rs].big.lft, tr[k].big.lftr = tr[rs].big.lftr;
    else tr[k].big.lft = tr[ls].big.lft, tr[k].big.lftr = tr[ls].big.lftr;
    //以上为左端点开始的最大子段和
    if(tr[rs].sum + tr[ls].big.rgt > tr[rs].big.rgt) tr[k].big.rgt = tr[rs].sum + tr[ls].big.rgt, tr[k].big.rgtl = tr[ls].big.rgtl;
    else tr[k].big.rgt = tr[rs].big.rgt, tr[k].big.rgtl = tr[rs].big.rgtl;
    //以上为右端点开始的最大子段和
    if(tr[ls].sml.ans < tr[rs].sml.ans) tr[k].sml.ans = tr[ls].sml.ans, tr[k].sml.ansl = tr[ls].sml.ansl, tr[k].sml.ansr = tr[ls].sml.ansr;
    else tr[k].sml.ans = tr[rs].sml.ans, tr[k].sml.ansl = tr[rs].sml.ansl, tr[k].sml.ansr = tr[rs].sml.ansr;
    if(tr[ls].sml.rgt + tr[rs].sml.lft < tr[k].sml.ans) tr[k].sml.ans = tr[ls].sml.rgt + tr[rs].sml.lft, tr[k].sml.ansl = tr[ls].sml.rgtl, tr[k].sml.ansr = tr[rs].sml.lftr;
    if(tr[ls].sum + tr[rs].sml.lft < tr[ls].sml.lft) tr[k].sml.lft = tr[ls].sum + tr[rs].sml.lft, tr[k].sml.lftr = tr[rs].sml.lftr;
    else tr[k].sml.lft = tr[ls].sml.lft, tr[k].sml.lftr = tr[ls].sml.lftr;
    if(tr[rs].sum + tr[ls].sml.rgt < tr[rs].sml.rgt) tr[k].sml.rgt = tr[rs].sum + tr[ls].sml.rgt, tr[k].sml.rgtl = tr[ls].sml.rgtl;
    else tr[k].sml.rgt = tr[rs].sml.rgt, tr[k].sml.rgtl = tr[rs].sml.rgtl;
    //以上为最小子段和的维护
}

void f(int k)
{
    swap(tr[k].big, tr[k].sml);
    tr[k].sum *= -1, tr[k].big.mul_1(), tr[k].sml.mul_1(), tr[k].tag ^= 1;
    return;
}

void pushdown(int k)
{
    if(!tr[k].tag) return;
    f(ls), f(rs);
    tr[k].tag = 0;
}

void build(int k, int l, int r)
{
    if(l == r)
    {
        tr[k].sum = a[l];
        tr[k].big.init(a[l], l), tr[k].sml.init(a[l], l);
        return;
    }
    int mid = l + r >> 1;
    build(ls, l, mid);
    build(rs, mid + 1, r);
    pushup(k);
}

void update(int k, int l, int r, int x, int v)
{
    if(l == r) return (void)(tr[k].big.init(v, -1), tr[k].sml.init(v, -1), tr[k].sum = v);
    pushdown(k);
    int mid = l + r >> 1;
    if(x <= mid) update(ls, l, mid, x, v);
    else update(rs, mid + 1, r, x, v);
    pushup(k);
}

void change(int k, int l, int r, int L, int R)
{
    if(L <= l && r <= R) return f(k);
    pushdown(k);
    int mid = l + r >> 1;
    if(L <= mid) change(ls, l, mid, L, R);
    if(R > mid) change(rs, mid + 1, r, L, R);
    pushup(k);
}

Node query(int k, int l, int r, int L, int R)
{
    if(L <= l && r <= R) return tr[k];
    pushdown(k);
    int mid = l + r >> 1;
    Node ll, rr, res;
    if(L <= mid && mid < R)
    {
        ll = query(ls, l, mid, L, R), rr = query(rs, mid + 1, r, L, R);
        res.sum = ll.sum + rr.sum;
        if(ll.big.ans > rr.big.ans) res.big.ans = ll.big.ans, res.big.ansl = ll.big.ansl, res.big.ansr = ll.big.ansr;
        else res.big.ans = rr.big.ans, res.big.ansl = rr.big.ansl, res.big.ansr = rr.big.ansr;
        if(ll.big.rgt + rr.big.lft > res.big.ans) res.big.ans = ll.big.rgt + rr.big.lft, res.big.ansl = ll.big.rgtl, res.big.ansr = rr.big.lftr;
        if(ll.sum + rr.big.lft > ll.big.lft) res.big.lft = ll.sum + rr.big.lft, res.big.lftr = rr.big.lftr;
        else res.big.lft = ll.big.lft, res.big.lftr = ll.big.lftr;    
        if(rr.sum + ll.big.rgt > rr.big.rgt) res.big.rgt = rr.sum + ll.big.rgt, res.big.rgtl = ll.big.rgtl;
        else res.big.rgt = rr.big.rgt, res.big.rgtl = rr.big.rgtl;
        if(ll.sml.ans < rr.sml.ans) res.sml.ans = ll.sml.ans, res.sml.ansl = ll.sml.ansl, res.sml.ansr = ll.sml.ansr;
        else res.sml.ans = rr.sml.ans, res.sml.ansl = rr.sml.ansl, res.sml.ansr = rr.sml.ansr;
        if(ll.sml.rgt + rr.sml.lft < res.sml.ans) res.sml.ans = ll.sml.rgt + rr.sml.lft, res.sml.ansl = ll.sml.rgtl, res.sml.ansr = rr.sml.lftr;
        if(ll.sum + rr.sml.lft < ll.sml.lft) res.sml.lft = ll.sum + rr.sml.lft, res.sml.lftr = rr.sml.lftr;
        else res.sml.lft = ll.sml.lft, res.sml.lftr = ll.sml.lftr;
        if(rr.sum + ll.sml.rgt < rr.sml.rgt) res.sml.rgt = rr.sum + ll.sml.rgt, res.sml.rgtl = ll.sml.rgtl;
        else res.sml.rgt = rr.sml.rgt, res.sml.rgtl = rr.sml.rgtl;
        return res;
    }
    //为了方便合并，当需要合并的时候我们直接合并，合并方式与 pushup 类似
    if(L <= mid) return query(ls, l, mid, L, R);
    if(R > mid) return query(rs, mid + 1, r, L, R);
}

思考：区间覆盖该怎么办？

等差子序列

【国家集训队】 等差子序列

给一个 \(1\) 到 \(N\) 的排列 \(\{A_i\}\)，询问是否存在

\[1 \le p_1<p_2<p_3<p_4<p_5<…<p_{Len} \le N (Len \ge 3)\]

使得 \(Ap_1,Ap_2,Ap_3,\cdots,Ap_{Len}\) 是一个等差序列。

\(1 \leq N \leq 5\times 10^5\)，\(5s\)。

只需要求出一个长度为 \(3\) 的等差子序列即可，即找到 \(i<j<k\)，使得 \(A_i,A_j,A_k\) 为等差序列。

一个很显然的套路是枚举中间值，判断是否存在 \(A_i=A_j-x(i<j)\) 和 \(A_k=A_j+x(k>j)\) 即可。

而因为 \(\{A_n\}\) 是排列，因此这两个数一定存在（合法情况下），且一定位于 \(A_j\) 的左侧或右侧。那我们不妨建立类似于值域线段树的东西，若 \(A_i\) 在 \(A_j\) 左侧，则第 \(A_i\) 叶子节点为 \(0\)，否则为 \(1\)。

显然，对于 \(A_j\)，想要不存在等差子序列，必须满足 \(A_{j-x}=A_{j+x}\)。那么对于区间 \([j-1,1],[j+1,n]\)，两者必须完全相同。（这里的 \([j-1,1]\) 表示序列 \(A_{j-1},A_{j-2}\cdots A_1\)）

怎么维护是否相同呢？字符串哈希！

线段树维护 \([l,r]\) 的哈希值即可！对于不同的 \(j\)，由于只会影响到至多两个点，因此单点修改即可。

（但是这题我写的树状数组，就不放代码了。）

双面棋盘

【WC2005】 双面棋盘

给定 \(n\times n\) 的 \(01\) 四连通矩阵（即，上下左右）。

每次取反一个数，求 \(0\)、\(1\) 连通块分别的数量。

\(1\leq n\leq 200,1\leq q\leq 10^4\)。

不加修改操作怎么做？并查集即可。

加上修改操作呢？只需要线段树维护并查集就可以了！

因此线段树套并查集，线段树节点维护 \([l,r]\) 行的并查集，合并的时候合并 \([l,mid]\) 与 \([mid + 1,r]\)，只需要暴力合并 \(mid,mid+1\) 即可。

单次合并用路径压缩+按秩合并并查集，时间复杂度 \(O(\alpha(n))\)，每次合并操作 \(O(n\alpha(n))\)，总复杂度 \(O(qn\alpha(n)\log n)\)。

Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
bool mp[MAXN][MAXN]; //0 wt 1 bk
int fa[MAXN * MAXN];
struct Tree
{
    int wt, bk;
    int l, r;
    int lson[MAXN], rson[MAXN];
}t[MAXN << 2];
int id(int x, int y) {return x * n + y;}

int get(int x) {return x == fa[x] ? x : fa[x] = get(fa[x]);}

void pushup(int k)
{
    for(int i = 1; i <= n; i++)
    {
        t[k].lson[i] = t[ls].lson[i];
        t[k].rson[i] = t[rs].rson[i];
        fa[t[ls].lson[i]] = t[ls].lson[i];
        fa[t[rs].lson[i]] = t[rs].lson[i];
        fa[t[ls].rson[i]] = t[ls].rson[i];
        fa[t[rs].rson[i]] = t[rs].rson[i];
    }
    t[k].bk = t[ls].bk + t[rs].bk;
    t[k].wt = t[ls].wt + t[rs].wt;
    int mid = (t[k].l + t[k].r) >> 1;
    for(int i = 1; i <= n; i++)
    {
        if(mp[mid][i] == mp[mid + 1][i])
        {
            int L = get(t[ls].rson[i]);
            int R = get(t[rs].lson[i]);
            if(L != R)
            {
                fa[L] = R;
                mp[mid][i] == 0 ? t[k].wt-- : t[k].bk--;
            }
        }
    }
    for(int i = 1; i <= n; i++)
    {
        t[k].lson[i] = get(t[k].lson[i]);
        t[k].rson[i] = get(t[k].rson[i]);
    }
}

void build(int k, int l, int r)
{
    t[k].l = l;
    t[k].r = r;
    if(l == r)
    {
        for(int i = 1; i <= n; i++)
        {
            t[k].lson[i] = id(l, i);
            t[k].rson[i] = id(l, i);
            fa[id(l, i)] = id(l, i);
            mp[l][i] == 0 ? t[k].wt++ : t[k].bk++;
        }
        for(int i = 2; i <= n; i++)
        {
            if(mp[l][i] == mp[l][i - 1])
            {
                t[k].lson[i] = fa[id(l, i - 1)];
                t[k].rson[i] = fa[id(l, i - 1)];
                fa[id(l, i)] = fa[id(l, i - 1)];
                mp[l][i] == 0 ? t[k].wt-- : t[k].bk--;
            }
        }
        return;
    }
    int mid = (l + r) >> 1;
    build(ls, l, mid);
    build(rs, mid + 1, r);
    pushup(k);
}

void update(int k, int p)
{
    if(t[k].l == t[k].r)
    {
        t[k].wt = 0;
        t[k].bk = 0;
        for(int i = 1; i <= n; i++)
        {
            t[k].lson[i] = id(p, i);
            t[k].rson[i] = id(p, i);
            fa[id(p, i)] = id(p, i);
            mp[p][i] == 0 ? t[k].wt++ : t[k].bk++;
        }
        for(int i = 2; i <= n; i++)
        {
            if(mp[p][i] == mp[p][i - 1])
            {
                t[k].lson[i] = fa[id(p, i - 1)];
                t[k].rson[i] = fa[id(p, i - 1)];
                fa[id(p, i)] = fa[id(p, i - 1)];
                mp[p][i] == 0 ? t[k].wt-- : t[k].bk--;
            }
        }
        return;
    }
    if(t[ls].r >= p) update(ls, p);
    if(t[rs].l <= p) update(rs, p);
    pushup(k);
}

决战圆锥曲线

【UR #8】决战圆锥曲线

给定伪随机序列 \(\{a_n\}\)，有三种操作：

  1. 给定 \(x,v\)，\(a_x\leftarrow v\)；

  2. 给定 \(l,r\)，\(\forall a_i\in[l,r],a_i\leftarrow 10^5-a_i\)；

  3. 给定 \(l,r,x,y,z\)，求 \(\max\limits_{i=l}^{r}\{xi+ya_i+zia_i\}\)。

\(1\leq n\leq 10^5,1\leq q\leq 10^6\)，\(2s\)。

操作 \(1,2\) 显然都是好做的，直接搞就可以了。

而对于操作 \(3\)，我们可以这么做：因为若 \(j<i\land a_j<a_i\)，则 \(j\) 必然不可能被选中。因此选择当前区间中 \(a_i\) 的最大值，之后查询所有 \(a_j(j>i)\) 即可。

分析一下时间复杂度：我们一次查询操作相当于再找上升子段。在随机数据的情况下，最长上升子段的长度期望近似于 \(O(\log n)\)，严格证明可以看这里。那么一次线段树的查询操作就是 \(O(\log^2 n)\)，总时间复杂度 \(O(q\log^2n)\)

Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
struct Node
{
    int minn, maxx;
    int tag;
}tr[MAXN << 2];

void pushup(int k)
{
    tr[k].maxx = max(tr[ls].maxx, tr[rs].maxx);
    tr[k].minn = min(tr[ls].minn, tr[rs].minn);
}

void f(int k)
{
    tr[k].tag ^= 1;
    swap(tr[k].maxx, tr[k].minn);
    tr[k].minn = mod4 - 1 - tr[k].minn;
    tr[k].maxx = mod4 - 1 - tr[k].maxx;
}

void pushdown(int k)
{
    if(!tr[k].tag) return;
    f(ls), f(rs);
    tr[k].tag = 0;
}

void build(int k, int l, int r)
{
    if(l == r) return (void)(tr[k].maxx = tr[k].minn = a[l]);
    int mid = l + r >> 1;
    build(ls, l, mid);
    build(rs, mid + 1, r);
    pushup(k);
}

void change(int k, int l, int r, int x, int v)
{
    if(l == r) return (void)(tr[k].maxx = tr[k].minn = v);
    pushdown(k);
    int mid = l + r >> 1;
    if(x <= mid) change(ls, l, mid, x, v);
    else change(rs, mid + 1, r, x, v);
    pushup(k);
}

void update(int k, int l, int r, int L, int R)
{
    if(L <= l && r <= R) return f(k);
    pushdown(k);
    int mid = l + r >> 1;
    if(L <= mid) update(ls, l, mid, L, R);
    if(R > mid) update(rs, mid + 1, r, L, R);
    pushup(k);
}

void query(int k, int l, int r, int L, int R, int x, int y, int z)
{
    if((res = x * r + y * tr[k].maxx + z * r * tr[k].maxx) <= ans) return;
    if(l == r) return (void)(ans = res);
    pushdown(k);
    int mid = l + r >> 1;
    if(R > mid) query(rs, mid + 1, r, L, R, x, y, z);
    if(L <= mid) query(ls, l, mid, L, R, x, y, z);
}

Rikka with Phi

HDU5634 Rikka with Phi

给定序列 \(\{a_n\}\)，\(q\) 次操作，诸如：

  1. 给定 \(l,r\)，\(\forall a_i\in [l,r],a_i\leftarrow \varphi(a_i)\)；

  2. 给定 \(l,r,x\)，\(\forall a_i\in[l,r],a_i\leftarrow x\)；

  3. 查询区间和。

\(1\leq n,q\leq 3\cdot 10^5,1\leq a_i\leq 10^7\)。

没有区间覆盖怎么做？

与区间开根类似。一个数 \(n\) 最多被 \(\varphi\) 过 \(\log n\) 次之后就会变成 \(1\)。那么我们暴力更改一个点的时间复杂度是 \(O(\log^2n)\) 的，总时间复杂度均摊为 \(O(n\log^2 n)\)。

那加上区间覆盖操作呢？区间覆盖有一个很重要的性质：经过操作之后，序列会被分成若干块。那么我们不妨维护一下当前区间是否相同，如果相同，求 \(\varphi\) 后还是相同。时间复杂度仍然是均摊的 \(O(n\log^2n)\)。

Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
int tree[MAXN << 2], andd[MAXN << 2];

int lc(int k){return k << 1;}

int rc(int k){return k << 1 | 1;}

void pushup(int k)
{
    tree[k] = tree[lc(k)] + tree[rc(k)];
    if(andd[lc(k)] == andd[rc(k)]) andd[k] = andd[lc(k)];
    else andd[k] = 0;
}

void pushdown(int k, int l, int r)
{
    if(andd[k])
    {
        int mid = (l + r) >> 1;
        andd[lc(k)] = andd[rc(k)] = andd[k];
        tree[lc(k)] = andd[lc(k)] * (mid - l + 1);
        tree[rc(k)] = andd[rc(k)] * (r - mid);
        andd[k] = 0;
    }
}

void build(int k,int l, int r)
{
    if(l == r)
    {
        tree[k] = andd[k] = a[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(lc(k), l, mid);
    build(rc(k), mid + 1, r);
    pushup(k);
}

void update(int k, int l, int r, int L, int R)
{
    if(L > R)
        return;
    if(andd[k] && l == L && r == R)
    {
        andd[k] = phi[andd[k]];
        tree[k] = andd[k] * (r - l + 1);
        return;
    }
    pushdown(k, l, r);
    int mid = (l + r) >> 1;
    if(R <= mid) update(lc(k), l, mid, L, R);
    else if(L > mid) update(rc(k), mid + 1, r, L, R);
    else
    {
        update(lc(k), l, mid, L, mid);
        update(rc(k), mid + 1, r, mid + 1, R);
    }
    pushup(k);
}

void update2(int k, int l, int r, int L, int R, int v)
{
    if(L > R)
        return;
    if(l == L && r == R)
    {
        andd[k] = v;
        tree[k] = andd[k] * (r - l + 1);
        return;
    }
    pushdown(k, l, r);
    int mid = (l + r) >> 1;
    if(R <= mid) update2(lc(k), l, mid, L, R, v);
    else if(L > mid) update2(rc(k), mid + 1, r, L, R, v);
    else
    {
        update2(lc(k), l, mid, L, mid, v);
        update2(rc(k), mid + 1, r, mid + 1, R, v);
    }
    pushup(k);
}

int query(int k, int l, int r, int L, int R)
{
    int res = 0;
    if(L <= l && r <= R) return tree[k];
    int mid = (l + r) >> 1;
    pushdown(k, l, r);
    if(R <= mid) return query(lc(k), l ,mid, L, R);
    else if(L > mid) return query(rc(k), mid + 1, r, L, R);
    else return query(lc(k), l ,mid, L, mid) + query(rc(k), mid + 1, r, mid + 1, R);
}

一年前写的代码，好丑。

Wall

【IOI2014】Wall

给定初始全部为 \(0\) 的序列 \(\{a_n\}\)，\(k\) 次操作：

  1. 给定 \(l,r,h\)，\(\forall a_i\in [l,r],a_i\leftarrow\min(a_i, h)\)；

  2. 给定 \(l,r,h\)，\(\forall a_i\in [l,r],a_i\leftarrow\max(a_i, h)\)；

\(1\leq n\leq 2\cdot 10^6,1\leq k\leq 5\cdot 10^5\)。

这题作为一道 IOI 题，感觉有点过于水了。

我们发现这两个操作实际上相当于划定了某个区间的上界和下界，\(1\) 操作是对上界的操作，相当于把 \(h\) 上面的数字都映射到 \(h\) 上，\(2\) 操作是对下界的操作。

既然这样，那么我们不妨维护一个当前区间上下界。合并很好合并，考虑一下如何修改。

先讨论上界的变动：

更改

如图，两条实线是我们目前的上下界，而我们更改的 \(h\) 有三种可能：高于上界（红色虚线）、在上下界间（绿色虚线）、低于下界（粉色虚线 （这到底是粉色还是紫色啊） ）。

第一种情况：高于上界。由于我们现在所有的数都在蓝线之间了，将上界拉高不会产生什么实质性的影响，因此上界不变。

第二种情况：在上下界间。此时在上蓝线与绿线中间的数字要被映射到绿线上，因此上界被压倒绿色虚线，更改上界。

第三种情况：低于下界。此时新更新的上界已经比原来的下界还要低了，现在所有的点都要被映射到粉线上，上下界都需要更改到粉线。

下界的变动也类似，按照上例讨论即可。最后的答案即是下界的值。

Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
struct Node
{
    int maxx, minn;
    int mxtg = -1, mntg = -1;
}tr[MAXN << 2];

void pushup(int k)
{
    tr[k].maxx = max(tr[ls].maxx, tr[rs].maxx);
    tr[k].minn = min(tr[ls].minn, tr[rs].minn);
}

void f1(int k, int v)
{
    tr[k].minn = max(tr[k].minn, v);
    tr[k].maxx = max(tr[k].maxx, tr[k].minn); 
    tr[k].mxtg = tr[k].maxx;
    tr[k].mntg = tr[k].minn;
}

void f2(int k, int v)
{
    tr[k].maxx = min(tr[k].maxx, v);
    tr[k].minn = min(tr[k].maxx, tr[k].minn); 
    tr[k].mxtg = tr[k].maxx;
    tr[k].mntg = tr[k].minn;
}

void pushdown(int k)
{
    if(tr[k].mntg != -1) f1(ls, tr[k].mntg), f1(rs, tr[k].mntg), tr[k].mntg = -1;
    if(tr[k].mxtg != -1) f2(ls, tr[k].mxtg), f2(rs, tr[k].mxtg), tr[k].mxtg = -1;
}

void add(int k, int l, int r, int L, int R, int v)
{
    if(L <= l && r <= R) return f1(k, v);
    pushdown(k);
    int mid = l + r >> 1;
    if(L <= mid) add(ls, l, mid, L, R, v);
    if(R > mid) add(rs, mid + 1, r, L, R, v);
    pushup(k);
}

void rmv(int k, int l, int r, int L, int R, int v)
{
    if(L <= l && r <= R) return f2(k, v);
    pushdown(k);
    int mid = l + r >> 1;
    if(L <= mid) rmv(ls, l, mid, L, R, v);
    if(R > mid) rmv(rs, mid + 1, r, L, R, v);
    pushup(k);
}

int query(int k, int l, int r, int x)
{
    if(l == r) return tr[k].minn;
    pushdown(k);
    int mid = l + r >> 1;
    if(x <= mid) return query(ls, l, mid, x);
    else return query(rs, mid + 1, r, x);
}

PS：一开始 query 的 if-else 没写 return，导致开了 \(O2\) 就会 RE。死因：有返回值函数不返回是 UB，警钟敲烂。

PS2：我宣布这个代码的区间修改函数是线段树区间修改函数最美丽的形态！！1

树状数组

【ZJOI2017】 树状数组

题面很难简述，看原题吧。

首先，题目给的树状数组并不是错误写法，而是一种经典的树状数组应用：将 query 和 add 的 lowbit 同时写反，原本对前缀的操作就会变成对后缀操作。

但是 query 函数中，他对于一段区间的操作仍然是 \(\text{Find}(r)-\text{Find}(l-1)\)，这就导致了我们查询的结果并不是 \([l,r]\)，而是向左偏移了一位，变成了 \([l-1,r-1]\)。

加 \(1\) 再取模 \(2\) 的操作相当于布尔型取反，的这意味着我们可以只关心 \(A_{l-1}\) 和 \(A_r\) 是否相同即可。

这里有一个理所当然的误区：我们可能很容易想到维护 \(B_i\) 表示第 \(i\) 个数为 \(1\) 的概率，那么对于一段长度为 \(len\) 的区间，每个数变成 \(1\) 的概率就会是 \(\dfrac{1}{len}\)。但是这时有一个反例：如果对于区间 \([1,2]\) 执行一次操作，\(B_1=B_2=\dfrac{1}{2}\)，此时如果暴力计算，\(A_1,A_2\) 相等的概率就变成了 \(\dfrac{1}{4}\)，然而实际上这个结果应该是 \(0\)。

这实际上断绝了我们直接考虑每个数的概率的可行性。

那么我们不妨维护每个点对 \((l,r)\) 表示 \(A_l,A_r\) 相等的概率。此时我们的操作区间可以分成三种：

  1. 只涵盖了一个点的区间：此时会产生 \(\dfrac{1}{len}\) 的影响。
  2. 涵盖了两个点的区间：此时会产生 \(\dfrac{2}{len}\) 的影响。
  3. 一个点都没涵盖的区间：不管。

此时有一个非常巧妙的做法：我们不妨将 \((l,r)\) 的点对看作一个二维网格，那么我们对于一次区间操作 \((L,R)\)，考虑他对每个点对的影响。

二维网格

举个例子：如上图，如果我们对原序列 \([3,5]\) 进行操作，那么第一种情况的点对对应的就是红色区域，第二种情况的点对对应的就是黄色区域，第三种情况对应的白色区域。

现在就显然可以用二维线段树（或者叫线段树套线段树）维护了。中间黄色三角形不太好维护，可以直接填满矩形。

不过还有一个问题：你发现这个树状数组的 \(\text{Find}\) 比一般的要长一点；因为他加了一个特判。当 \(l=1\) 的时候，\(x\) 会变成 \(0\)，此时会直接返回 \(0\)，相当于问你区间 \([r,n]\) 是否为 \(0\) 了，特别处理一下即可。

时空复杂度均为 \(O(n\log^2 n)\)。

Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
int rt[MAXN << 2], lson[MAXN * 375], rson[MAXN * 375], res[MAXN * 375];
int n, m, cnt;

int qpow(ll x, int y)
{
    ll ans = 1;
    for(; y; x = x * x % mod, y >>= 1) if(y & 1) ans = ans * x % mod;
    return ans % mod;
}

int calc(int p, int q){return (1ll * p * q % mod + 1ll * ((1 + mod - p) % mod) * ((1 + mod - q) % mod) % mod) % mod;}

void update(int &k, int l, int r, int L, int R, int v)
{
    if(!k) k = ++cnt, res[k] = 1;
    if(L <= l && r <= R) return (void)(res[k] = calc(res[k], v));
    int mid = (l + r) >> 1;
    if(L <= mid) update(lson[k], l, mid, L, R, v);
    if(R > mid) update(rson[k], mid + 1, r, L, R, v);
}

void Update(int k, int l, int r, int L1, int R1, int L2, int R2, int v)
{
    if(L1 <= l && r <= R1) return update(rt[k], 1, n, L2, R2, v);
    int mid = (l + r) >> 1;
    if(L1 <= mid) Update(ls, l, mid, L1, R1, L2, R2, v);
    if(R1 > mid) Update(rs, mid + 1, r, L1, R1, L2, R2, v);
}

int query(int k, int l, int r, int x)
{
    if(!k) return 1;
    if(l == r) return res[k];
    int mid = (l + r) >> 1;
    if(x <= mid) return calc(res[k], query(lson[k], l, mid, x));
    else return calc(res[k], query(rson[k], mid + 1, r, x));
}

int Query(int k, int l, int r, int x1, int x2)
{
    if(l == r) return query(rt[k], 1, n, x2);
    int mid = (l + r) >> 1;
    if(x1 <= mid) return calc(query(rt[k], 1, n, x2), Query(ls, l, mid, x1, x2));
    else return calc(query(rt[k], 1, n, x2), Query(rs, mid + 1, r, x1, x2));
}

signed main()
{
    read(n, m);
    while(m--)
    {
        int op, l, r;
        read(op, l, r);
        if(op == 1)
        {
            int x = qpow(r - l + 1, mod - 2);
			if(l > 1)
            {
                Update(1, 0, n, 1, l - 1, l, r, (1 + mod - x) % mod);
                Update(1, 0, n, 0, 0, 1, l - 1, 0);
            }
			if(r < n)
            {
                Update(1, 0, n, l, r, r + 1, n, (1 + mod - x) % mod);
                Update(1, 0, n, 0, 0, r + 1, n, 0);
			}
            Update(1, 0, n, l, r, l, r, (1 + 2ll * mod - 2ll * x) % mod);
            Update(1, 0, n, 0, 0, l, r, x);
        }
        else printf("%d\n", Query(1, 0, n, l - 1, r));
    }
    return 0;
}

楼房重建

洛谷P4198 楼房重建

在一个二维平面上有 \(N\) 栋楼房。小 A 在平面上 \((0,0)\) 点的位置，第 \(i\) 栋楼房可以用一条连接 \((i,0)\) 和 \((i,H_i)\) 的线段表示，其中 \(H_i\) 为第 \(i\) 栋楼房的高度。如果这栋楼房上任何一个高度大于 \(0\) 的点与 \((0,0)\) 的连线没有与之前的线段相交，那么这栋楼房就被认为是可见的。

施工队的建造总共进行了 \(M\) 天。初始时，所有楼房都还没有开始建造，它们的高度均为 \(0\)。在第 \(i\) 天，建筑队将会将横坐标为 \(X_i\) 的房屋的高度变为 \(Y_i\)。请你帮小 A 数数每天在建筑队完工之后，他能看到多少栋楼房?

\(1 \le X_i \le N\)，\(1 \le Y_i \le 10^9\)，\(1\le N,M \le 10^5\)。

根据我们小学二年级学过的几何知识，我们可以把这个题目转化一下：题目等同于维护 \((i,H_i)\) 到 \((0,0)\) 连线的斜率 \(k_i\)，并求出从 \(1\) 开始、贪心的上升子序列（即如果当前点大于最大值，则一定选取它）。

考虑用线段树去维护它。考虑怎么把两端信息合并。

首先，左区间和右区间合并的时候，左区间一定全选，而右区间会选择大于左区间 \(max\) 的部分。这个东西怎么求？

线段树二分！

我们只需要在合并的时候同时二分右区间即可。时间复杂度 \(O(n\log^2 n)\)。

Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int get(int k, int l, int r, double x)
{
    if(tr[k].maxx <= x) return 0;
    if(l == r) return (tr[k].maxx > x);
    int mid = (l + r) >> 1;
    if(tr[ls].maxx <= x) return get(rs, mid + 1, r, x);
    return get(ls, l, mid, x) + tr[k].len - tr[ls].len;
}

void pushup(int k, int l, int r)
{
    int mid = (l + r) >> 1;
    tr[k].len = tr[ls].len + get(rs, mid + 1, r, tr[ls].maxx);
    tr[k].maxx = max(tr[ls].maxx, tr[rs].maxx);
}

void update(int k, int l, int r, int x, int v)
{
    if(l == x && r == x) return (void)(tr[k].maxx = 1.00 * v / x, tr[k].len = 1);
    int mid = (l + r) >> 1;
    if(x <= mid) update(ls, l, mid, x, v);
    else update(rs, mid + 1, r, x, v);
    pushup(k, l, r);
}

大魔法师

【THUSCH2017】 大魔法师

如果是互不影响的几个值，那么用线段树很好维护。但是现在是几个相互影响的值，考虑该怎么办。

一个非常巧妙的想法是用矩阵维护这些关系。我们把每个水晶球看作一个行向量 \((A_i,B_i,C_i,v)\)，前三者表示不同的属性，第四者是常数项，初始为 \(1\)，表示区间元素个数。

那么我们推出来各个操作的转移矩阵：

\[ \text{Opt}_1=\begin{bmatrix} 1 & 0 & 0 & 0\\ 1 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \] \[ \text{Opt}_2=\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 1 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \] \[ \text{Opt}_3=\begin{bmatrix} 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \] \[ \text{Opt}_4=\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ v & 0 & 0 & 1 \end{bmatrix} \] \[ \text{Opt}_5=\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & v & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \] \[ \text{Opt}_6=\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & v & 1 \end{bmatrix} \]

然后直接用线段树维护矩阵就可以了。

但是这题有些卡常，这里有一些可以使用的卡常技巧：

  1. 循环展开：将矩阵加法和乘法最内层的循环展开，可以优化大量时间；
  2. 注意到我们实际维护的只是一个行向量，因此没有必要按照 \(4\times 4\) 矩阵维护；
  3. 不要开 long long。
Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
struct Matrix
{
    int a[4][4];

    Matrix() {memset(a, 0, sizeof(a));}

    void clear() {memset(a, 0, sizeof(a));}

    void getI()
    {
        memset(a, 0, sizeof(a));
        a[0][0] = a[1][1] = a[2][2] = a[3][3] = 1;
    }

    Matrix operator+ (Matrix &A) const
    {
        Matrix B;
        for(int i = 0; i < 4; i++)
        {
            B.a[i][0] = (a[i][0] + A.a[i][0]) % mod;
            B.a[i][1] = (a[i][1] + A.a[i][1]) % mod;
            B.a[i][2] = (a[i][2] + A.a[i][2]) % mod;
            B.a[i][3] = (a[i][3] + A.a[i][3]) % mod;
        }
        return B;
    }

    Matrix operator* (Matrix &A) const
    {
        Matrix B;
        for(int i = 0; i < 4; i++)
        {
            for(int j = 0; j < 4; j++)
            {
                B.a[i][j] = (B.a[i][j] + (1ll * a[i][0] * A.a[0][j]) % mod) % mod;
                B.a[i][j] = (B.a[i][j] + (1ll * a[i][1] * A.a[1][j]) % mod) % mod;
                B.a[i][j] = (B.a[i][j] + (1ll * a[i][2] * A.a[2][j]) % mod) % mod;
                B.a[i][j] = (B.a[i][j] + (1ll * a[i][3] * A.a[3][j]) % mod) % mod;
            }
        }
        return B;
    }

    bool operator== (Matrix &A) const
    {
        for(int i = 0; i < 4; i++)
        {
            if(A.a[i][0] != a[i][0]) goto FALSE;
            if(A.a[i][1] != a[i][1]) goto FALSE;
            if(A.a[i][2] != a[i][2]) goto FALSE;
            if(A.a[i][3] != a[i][3]) goto FALSE;
        }
        return true;
        FALSE:return false;
    }
};

Matrix opt[7], I;
int A[MAXN], B[MAXN], C[MAXN];
int n, m;

struct Node
{
    Matrix sum, tag;
}tr[MAXN << 2];

void init()
{
    for(int i = 1; i <= 6; i++) opt[i].getI();
    opt[1].a[1][0] = 1;
    opt[2].a[2][1] = 1;
    opt[3].a[0][2] = 1;
}

void pushup(int k)
{
    tr[k].sum = tr[ls].sum + tr[rs].sum;
}

void pushdown(int k)
{
    if(tr[k].tag == I) return;
    tr[ls].sum = tr[ls].sum * tr[k].tag;
    tr[rs].sum = tr[rs].sum * tr[k].tag;
    tr[ls].tag = tr[ls].tag * tr[k].tag;
    tr[rs].tag = tr[rs].tag * tr[k].tag;
    tr[k].tag.getI();
}

void build(int k, int l, int r)
{
    tr[k].tag.getI();
    if(l == r)
    {
        tr[k].sum.a[0][0] = A[l];
        tr[k].sum.a[0][1] = B[l];
        tr[k].sum.a[0][2] = C[l];
        tr[k].sum.a[0][3] = 1;
        return;
    }
    int mid = (l + r) >> 1;
    build(ls, l, mid);
    build(rs, mid + 1, r);
    pushup(k);
}

void update(int k, int l, int r, int L, int R, Matrix v)
{
    if(L <= l && r <= R)
    {
        tr[k].sum = tr[k].sum * v;
        tr[k].tag = tr[k].tag * v;
        return;
    }
    pushdown(k);
    int mid = (l + r) >> 1;
    if(L <= mid) update(ls, l, mid, L, R, v);
    if(R > mid) update(rs, mid + 1, r, L, R, v);
    pushup(k);
}

Matrix query(int k, int l, int r, int L, int R)
{
    Matrix Ans;
    if(L <= l && r <= R) return tr[k].sum;
    pushdown(k);
    int mid = (l + r) >> 1;
    if(L <= mid) Ans = query(ls, l, mid, L, R) + Ans;
    if(R > mid) Ans = query(rs, mid + 1, r, L, R) + Ans;
    return Ans;
}

signed main()
{
    init();
    I.getI();
    read(n);
    for(int i = 1; i <= n; i++) read(A[i], B[i], C[i]);
    build(1, 1, n);
    read(m);
    while(m--)
    {
        int op, l, r, v;
        read(op, l, r);
        if(op == 1) update(1, 1, n, l, r, opt[1]);
        else if(op == 2) update(1, 1, n, l, r, opt[2]);
        else if(op == 3) update(1, 1, n, l, r, opt[3]);
        else if(op == 4) read(v), opt[4].a[3][0] = v, update(1, 1, n, l, r, opt[4]);
        else if(op == 5) read(v), opt[5].a[1][1] = v, update(1, 1, n, l, r, opt[5]);
        else if(op == 6) read(v), opt[6].a[3][2] = v, opt[6].a[2][2] = 0, update(1, 1, n, l, r, opt[6]);
        else
        {
            Matrix ans = query(1, 1, n, l, r);
            printf("%d %d %d\n", ans.a[0][0], ans.a[0][1], ans.a[0][2]);
        }
    }
    return 0;
}

EI 的第六分块

洛谷P5693 EI 的第六分块

给定一个整数序列 \(a\)，支持两种操作：

  1. 1 l r x 表示给区间 \([l,r]\) 中每个数加上 \(x\)；

  2. 2 l r 表示查询区间 \([l,r]\) 的最大子段和（可以为空）。

\(1\le n,q \le 4\times 10^5\)，\(|a_i| \le 10^9\)，\(1 \le x \le 10^6\)。

虽然题目名字叫分块，但是我叛逆！

这道题是 KTT 板题。

首先，朴素的不带修区间最大子段和是很经典的。我们仿照这个问题，依旧维护 \(sum,ans,pre,suf\) 表示区间和、区间最大子段和、前缀最大子段和、后缀最大子段和。

现在每个变量不再是一个值，而是一个一次函数 \(y=kx+b\)，我们简记为 \((k,b)\)。其中 \(k\) 表示当前区间的长度，\(b\) 表示初始值。

如果一次操作之后，区间最优函数没有改变，即修改没有达到最近切换点，那么答案直接变成 \((kx,b)\) 即可。

如果当前操作使得区间最优函数改变，那么就直接暴力向下递归。

现在考虑如何合并。加入我们现在分别有 \(p=(k_p,b_p),q=(k_q,b_q)\)。不难发现，最近切换点就是两个一次函数的交点。如果焦点在 \(x\) 负半轴，记为 \(\inf\) 即可。

当一次修改超过最近切换点，那么 \(ans,pre,suf\) 其中至少一个会被改变，取 \(\min\) 即可。

具体复杂度分析，详见 EI's Blog。

Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
struct Func
{
    int k;
    int b;
    friend Func operator+(const Func &A, const Func &B) {return {A.k + B.k, A.b + B.b};}
    void add(int x) {b += k * x;}
};

pair<Func, int> max(Func A, Func B)
{
    if(A.k < B.k || A.k == B.k && A.b < B.b) swap(A, B);
    if(A.b >= B.b) return mp(A, INF);
    else return mp(B, (B.b - A.b) / (A.k - B.k));
}

struct KTT
{
    Func sum, ans, pre, suf;
    int th;
    friend KTT operator+(const KTT &A, const KTT &B)
    {
        KTT res;
        pair<Func, int> tmp;
        res.th = min(A.th, B.th);
        tmp = max(A.pre, A.sum + B.pre);
        res.pre = tmp.fi;
        res.th = min(res.th, tmp.se);
        tmp = max(B.suf, B.sum + A.suf);
        res.suf = tmp.fi;
        res.th = min(res.th, tmp.se);
        tmp = max(A.ans, B.ans);
        res.th = min(res.th, tmp.se);
        tmp = max(tmp.fi, A.suf + B.pre);
        res.ans = tmp.fi;
        res.th = min(res.th, tmp.se);
        res.sum = A.sum + B.sum;
        return res;
    }
    
    void add(int v)
    {
        sum.add(v), ans.add(v), pre.add(v), suf.add(v);
    }
};

struct Node
{
    KTT a;
    int tag;
}tr[MAXN << 2];

int n, Q, A[MAXN];

void pushup(int k)
{
    tr[k].a = tr[ls].a + tr[rs].a;
}

void f(int k, int v)
{
    tr[k].tag += v;
    tr[k].a.th -= v;
    tr[k].a.add(v);
}

void pushdown(int k)
{
    if(tr[k].tag == 0) return;
    f(ls, tr[k].tag), f(rs, tr[k].tag);
    tr[k].tag = 0;
}

void build(int k, int l, int r)
{
    if(l == r)
    {
        Func c = {1, A[l]};
        tr[k].a = {c, c, c, c, INF};
        return;
    }
    int mid = (l + r) >> 1;
    build(ls, l, mid);
    build(rs, mid + 1, r);
    pushup(k);
}

void defeat(int k, int v)
{
    if(v <= tr[k].a.th) return f(k, v);
    defeat(ls, tr[k].tag + v);
    defeat(rs, tr[k].tag + v);
    tr[k].tag = 0;
    pushup(k);
}

void update(int k, int l, int r, int L, int R, int v)
{
    if(L <= l && r <= R) return defeat(k, v);
    pushdown(k);
    int mid = (l + r) >> 1;
    if(L <= mid) update(ls, l, mid, L, R, v);
    if(R > mid) update(rs, mid + 1, r, L, R, v);
    pushup(k);
}

KTT query(int k, int l, int r, int L, int R)
{
    if(L <= l && r <= R) return tr[k].a;
    pushdown(k);
    int mid = (l + r) >> 1;
    if(R <= mid) return query(ls, l, mid, L, R);
    if(L > mid) return query(rs, mid+ 1, r, L, R);
    return query(ls, l, mid, L, mid) + query(rs, mid + 1, r, mid + 1, R);
}

火事（待做）

【JOI2020Final】 火事

给定一个长为 \(N\) 的序列 \(S_i\)，刚开始为时刻 \(0\)。定义 \(t\) 时刻第 \(i\) 个数为 \(S_i(t)\)，且满足：

\[\left\{ \begin{array}{ll} S_0(t)=0\\S_i(0)=S_i\\S_i(t)=\max\{S_{i-1}(t-1),S_i(t-1)\} \end{array} \right.\]

\(Q\) 次询问，每次给定 \(L,R,T\)，求：

\[\sum\limits_{k=L}^{R}S_k(T)\]

\(1\leq N,Q\leq 2\cdot 10^5\)。

参考与鸣谢

参考

  1. 《妈妈再也不用担心我的线段树了》——孙耀峰；
  2. OI Wiki；
  3. do_while_true 的李超树博客；
  4. RainAir 在 SDSC2023 上的课件；
  5. 碎月关于 KTT 的知乎文章；
  6. 《浅谈函数最值的动态维护》——李白天。

鸣谢

  1. EXODUS 对本文的勘误与启示；
  2. do_while_true 针对李超线段树的指导。
  • 标题: 线段树浅记
  • 作者: 夏佑 | XiaU
  • 创建于 : 2023-07-23 00:00:00
  • 更新于 : 2024-11-07 09:43:12
  • 链接: https://oi.xiau.ren/Segment-Tree/
  • 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。
此页目录
线段树浅记
  1. 1. 线段树
    1. 1.1. 结构
    2. 1.2. 信息的上传
    3. 1.3. 建树
    4. 1.4. 单点修改
    5. 1.5. 区间查询
    6. 1.6. 区间修改与懒标记
  2. 2. 线段树提高
    1. 2.1. 维护区间平方和
    2. 2.2. 区间乘与区间加
    3. 2.3. 区间开根
    4. 2.4. 维护前前缀和
    5. 2.5. 区间加等差数列
    6. 2.6. 维护区间最大子段和
  3. 3. 信息的本质
  4. 4. 线段树的本质
  5. 5. 线段树的常用技巧
    1. 5.1. 动态开点
    2. 5.2. 标记永久化
    3. 5.3. 线段树二分
  6. 6. 线段树进阶
    1. 6.1. 值域线段树
    2. 6.2. 扫描线
      1. 6.2.1. 线段树维护矩形面积并
      2. 6.2.2. 本质
    3. 6.3. 李超线段树
    4. 6.4. zkw 线段树
      1. 6.4.1. 结构
      2. 6.4.2. 建树
      3. 6.4.3. 单点修改、区间查询
      4. 6.4.4. 区间修改、区间查询
  7. 7. 多线段树操作
    1. 7.1. 线段树合并
    2. 7.2. 线段树分裂
  8. 8. 主席树
    1. 8.1. 简介
    2. 8.2. 结构
    3. 8.3. 操作
    4. 8.4. 区间修改
  9. 9. 线段树再进阶
    1. 9.1. 吉司机线段树
    2. 9.2. Kinetic Tournament Tree
  10. 10. 题目随解
    1. 10.1. k-Maximum Subsequence Sum
    2. 10.2. 等差子序列
    3. 10.3. 双面棋盘
    4. 10.4. 决战圆锥曲线
    5. 10.5. Rikka with Phi
    6. 10.6. Wall
    7. 10.7. 树状数组
    8. 10.8. 楼房重建
    9. 10.9. 大魔法师
    10. 10.10. EI 的第六分块
    11. 10.11. 火事（待做）
  11. 11. 参考与鸣谢
    1. 11.1. 参考
    2. 11.2. 鸣谢